Exploration 3.3.1.
Check the illustration below explaining more about Area (\(m^2\)).
Section 3.3 Area
Why area?
Area is the region bounded by the shape of an object.
We calculate areas of different objects eg. triangle, rectangle, squre,circle, and many more.
Subsection 3.3.1 Square metres\((m^2)\text{,}\)acres and hectares
Subsubsection 3.3.1.1 Square metres\((m^2)\)
Activity 3.3.2.
Work in pairs.
-
Fill in the table below
Lenght of square area \(1\,m\) \(10\,m\) \(25\,m\) -
Share your work with learners in your class.
Example 3.3.1.
Fill in the table below.
| Length of square | area |
|---|---|
| \(1\,m\) | |
| \(10\,m\) | |
| \(25\,m\) |
Subsubsection 3.3.1.2 Acres
-
Note that:
-
Another unit of measurering area is \(are\text{.}\)Therefore;\(4\,046.86\,m^2=1 \,\text{are}\)
Subsubsection 3.3.1.3 Hectares
A hectare is a unit of measuring large areas.
One hectare is equal to \(10\,000\, m^2\)
Therefore,
\(1 \,\text{hectare}(ha) = 10\,000\,m^2\)
\(1 \,\text{hectare}(ha) = 2.47 \,\text{acre}\)
Example 3.3.2.
Example 3.3.3.
Find the area of the figure below in hectares.
Solution.
Area of a square
\begin{align*}
=\amp \text{side} \times \text{side} \\
=\amp 600m \times 600m\\
=\amp 360\,000m^2
\end{align*}
Convert \(360\,000 m^2\) to hectares.
\begin{align*}
10 \,000m^2=\amp 1 ha\\
360\,000 m^2=\amp (360\,000 \div 10\,000) \text{hectares} \\
=\amp 36\, \text{hectares}
\end{align*}
The area of the figure is \(36 \) hectares
Subsection 3.3.2 Area of a rectangle
Activity 3.3.3.
Work in groups
-
Trace and cut out the rectangle below.
-
Find the area of the rectangle paper cut-out
-
Find the area of the rectangles below by multiplying the length and width.
Rectangles Length Width Area A \(8\,m\) \(5\,m\) \(\) B \(13\,cm\) \(7\,cm\) \(\) C \(21\,m\) \(18\,m\) \(\) D \(16\,cm\) \(11\,cm\) \(\) -
Share your answer with other learners in class.
Activity 3.3.4.
Play along with the activities below.
Build your own figures on a grid using unit squares to explore areas of rectangles, squares, and composite shapes in this activity
Calculate the areas of the figures given their side lengths.
Example 3.3.6.
Example 3.3.7.
Solution.
1.Find the area in \(m^2\) that is
\begin{align*}
\text{Area}= \amp \text{length}\times \text{width}\\
=\amp 300\,m \times 100\,m\\
=\amp 30000\,m^2
\end{align*}
2. Converting to \(ha\)
\begin{align*}
\text{if} \,1\, \text{ha}=\amp 10\,000m^2\\
30\,000\,m^2=\amp \frac{30\,000\,m^2 \times 1 ha }{10\,000\,m^2} \\
=\amp 3\,ha
\end{align*}
Example 3.3.8.
Work out the area of the figure below.
Subsection 3.3.3 Area of a parallelogram
-
Rectangle is a type of parallelogram where all the angles are 90°
-
All rectangles are parallelograms, but not all parallelograms are rectangles.
\begin{align*}
\text{Area of a parallelogram} = \amp \text{base} \times \text{height}\\
= \amp bh
\end{align*}
The figure below shows a parallelogram with base and height labeled.
Activity 3.3.5.
Work in pairs.
In this worksheet there two polygons; a rectangle and a parallelogram. Use the polygons to complete the investigation below.
-
Change the height of the rectangle (h) by moving point C. What happens to the height of the parallelogram?
-
Change the width of the rectangle by moving point L. What happens to the parallelogram?
-
Find the area of 3 different rectangles and compare the area of each rectangle to the area of the corresponding parallelogram.
-
What conjecture can you make about the formula for area of a parallelogram and why? (use the answer to question 3 to guide you)
-
Share your work with other leaners in class
Example 3.3.10.
Muchemi’s piece of land is in the shape below.
What is the area of the piece of land?
Example 3.3.11.
Mr Onyango’s garden is in the shape of a parallelogram. The length of the farm is \(42\,m\) and its height is \(21\,m\text{.}\) Find the area of the garden.
Hint.
Solution.
Given that the length \(= 42\,m\)
height of the farm \(= 21\,m\)
The scetch is as shown,
\begin{align*}
\text{Area of a parallelogram}=\amp \text{Base length} \times \text{Perpendicular height} \\
=\amp 42\,m \times 21\,m\\
=\amp 882\,m^2
\end{align*}
The area of the piece of garden is \({\color{blue} 882\,m^2}\text{.}\)
\({\textbf{ NOTE}}:\)
-
When calculating the area of a parallelogram ensure you use the formula Area \(= base \times height\)
-
For any drawn figure ensure you’ve obtained both the base and height before incoopereting the formula.
Subsection 3.3.4 Area of a rhombus
A rhombus is a type of quadrilateral that is a special kind of parallelogram. The key characteristics of a rhombus are:
-
Opposite sides are parallel.
-
All sides have equal length.
-
Opposite angles are equa and adjacent angles are supplementary (they add up to \(180°\)).
-
The diagonals of a rhombus bisect each other at right angles (90°), meaning they intersect at a right angle and divide each other into two equal parts.
The formula for the area \(A\) of a rhombus can be given in two common ways:
-
where:
-
Where the base is the length of any side (since all sides are equal) and the height is the perpendicular distance between opposite sides.
Activity 3.3.6.
Example 3.3.13.
Example 3.3.14.
Calculate the area of each rhombus.
Solution.
(a)
Area of a rhombus by the base and height: \(A= \text{base} \times \text{height}{}\text{.}\)
\begin{align*}
A= \amp \text{base} \times \text{height}\\
=\amp 5m \times 4m \\
= \amp 20m^2
\end{align*}
(b)
\begin{align*}
A= \amp \text{base} \times \text{height} \\
=\amp 9cm \times 7cm \\
= \amp 63cm^2
\end{align*}
Subsection 3.3.5 Area of trapeziam
The trapezium is a quadrilateral with one pair of parallel opposite sides. The parallel sides of a trapezium are called bases and the non-parallel sides of a trapezium are called legs. It is also called a trapezoid. Sometimes the parallelogram is also called a trapezoid with two parallel sides.
From the above figure, we can see, sides AB and CD are parallel to each other whereas AD and BC are non-parallel sides. Also, ‘h’ is the distance between the two parallel sides which demonstrates the height of the trapezium.
There are many real-life examples of trapezium shape that we can see around us. For example, a table whose surface is shaped like a trapezium.
-
\({\color{black}\textbf{Trapezium Formula}}\)Area of Trapezium \(=\frac{1}{2}(\text{Sum of parallel side})\,(\text{Distance between parallel sides})\)Which can be written as A\(= \frac{1}{2} (a+b)h\)where: \((a+b)\) is the sum of the parallel sides and \(h\) is the perpendicular height of the trapezium.
Activity 3.3.7.
-
First can you work out the formula for the area of a trapezium?Rotate out a second trapezium for a clue.Compare the shape to the formula for a parallelogram.Check your answer with the "show area formula" box.
-
Second can you change the shape (using the 3 blue corner dots and the height dot) to make other shapes?See if you can find a rhombus, parallelogram, rectangle, square and any tyoe of triangle.How does the formula change for the different shapes? Look at the values for a and b on the shape and in the formula.Use the rotate slider to see that it’s still always a parallelogram.
Example 3.3.16.
Harriate’s plot is in the shape of the figure below.
What is the area of the plot of land?
Example 3.3.17.
Calculate the area of a trapezium whose parallel sides are \(9cm\) and \(11cm\) and the vertical height is \(5cm\)
Example 3.3.18.
Find the length marked \(h\) in the figure.
Subsection 3.3.6 Area of a circle
A circle is a closed two-dimensional figure in which the set of all the points in the plane is equidistant from a given point called “centre”.
The diameter of the circle divides it into two equal parts.
\({\color{black}\textbf{Circle Formula.}}\)
Area of a circle is the amount of space occupied by the circle.
The circle formula to find the area is given by \(\text{Area of a circle}= \pi r^2\) where, \(r\) is the radius of the circle and \(\pi=\frac{22}{7} \,\text{or} \, 3.142 \text{.}\)
Activity 3.3.8.
\({\color{black}\textbf{Work in groups}}\)
-
You will need a pair of scissors, a pair of compusses and a manila paper.
-
Using the pair of campasses, draw a circle whose radius is \(7\,cm\text{.}\)What is the circumference of the circle?
-
Divide the circle into \(16\) equal sectors. Colour half of the sectors as shown below.
-
Cut out the sector and paste them on a manila paper as shown below.
-
What kind of a shape is formed?
-
What is the area of the shape formed?
-
How does the length of the rectangle compare to the circumference of the circle?
-
How does the width of the rectangle compare to the radius of the circle ?
-
Share your work with other learners in class.
Activity 3.3.9.
Interact with the app below for a few minutes. Then answer the questions that follow.
-
Figure 3.3.19. Area of a circle. What do you notice? What do you see? What do you wonder?How can we use what we see here to try to find the area of a circle?
Determine the dimensions of a circle using the the formula for the area of a circle and a given area value.
\({\textbf{Learning point}}\)
The figure formed resembles a rectangle.
The length of the rectangle is almost equal to \(\frac{1}{2}\) thecircumference of the circle, while the width is almost equal to to the radius of the circle.
\begin{align*}
\text{The area of the rectangle } =\amp \text{Length} \times \text{Width} \\
= \amp \frac{1}{2}\, \text{circumference} \times \text{ radius}
\end{align*}
The circumference of a circle is \(2 \pi r\text{.}\) This means that the length of the rectangle. is
\begin{equation*}
\frac{1}{2} \times 2 \pi r=\pi r
\end{equation*}
\begin{align*}
\text{The area of the circle }=\amp \pi r \times r \\
=\amp {\color{blue} \pi r^2}
\end{align*}
Example 3.3.21.
Fill in the table bellow. \((\text{Take} \pi = \frac{22}{7})\)
| Circle | Diameter | Radius | Area |
|---|---|---|---|
| a) | 49cm | ||
| b) | 7cm | ||
| c) | 21cm | ||
| d) | 35cm |
Solution.
The solution is as below:
| Circle | Diameter | Radius | Area |
|---|---|---|---|
| a) | \(49 \times 2=98cm \) | 49cm | \(\frac{22}{7} \times 49^2cm^2=7546cm^2\) |
| b) | 7cm | \(\frac{7}{2}=3.5cm\) | \(\frac{22}{7} \times 3.5^2cm^2=39.28cm^2\) |
| c) | 21cm | \(\frac{21}{2}=10.5cm\) | \(\frac{22}{7} \times 10.5^2cm^2=3465cm^2\) |
| d) | \(35 \times 2=70cm\) | 35cm | \(\frac{22}{7} \times 35^2cm^2=3850cm^2\) |
Example 3.3.22.
Find the area of the circle below.
Example 3.3.23.
Subsection 3.3.7 Area of a semicircle
A semicircle is a circle divided into two equal parts.
Since we now know the area of a circle, the area of a semicircle is the area of a circle divided by two as shown bellow;
\(\text{Area of semicircle}=\frac{1}{2} \times \pi r^2\text{.}\)
Example 3.3.24.
Find the area of the semicircle given below.
Solution.
\begin{align*}
\text{radius} =\amp \frac{\text{diameter}}{2} \\
r=\amp \frac{28}{2}cm \\
r=\amp 14cm
\end{align*}
\begin{align*}
\text{Area of semicircle}=\amp \frac{1}{2} \pi \times r^2 \\
=\amp \frac{1}{2} \pi \times r \times r\\
=\amp\frac{1}{2}\times\frac{22}{7} \times 14^2cm^2 \\
=\amp \frac{1}{2} \times\frac{22}{7} \times 196 cm^2\\
=\amp\frac{1}{2} \times 616cm^2 \\
=\amp 308cm^2
\end{align*}
Subsection 3.3.8 Area of borders and combined shapes
This section combines all the figures we have done and its requred that you are in a position to calculate areas of any figure given.
-
Combine figures can either be circle inside a circle, rectangle inside a rectangle, circle inside a trapezium and many more.
-
Its requred to calculate areas acording to the instractions given in an equation.
Some worked examples are as below.
Example 3.3.25.
Work out the area of the figure bellow.
Solution.
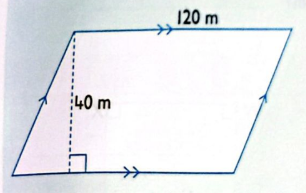
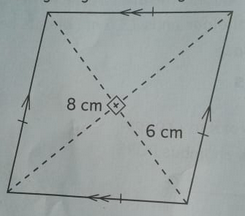
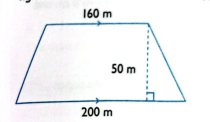
\begin{align*}
\text{Area of the rectangle}=\amp l \times w \\
=\amp 20cm \times 14cm \\
=\amp280 cm^2
\end{align*}
\begin{align*}
\text{Area of the triangle}=\amp \frac{1}{2} bh \\
=\amp \frac{1}{2} \times 18cm \times 14cm \\
= \amp 126cm^2
\end{align*}
\begin{align*}
\text{Area of the semicircle}=\amp \frac{1}{2} \pi r^2 \\
=\amp \frac{1}{2} \frac{22}{7} \times 7cm \times 7cm\\
=\amp77cm^2
\end{align*}
\begin{align*}
\text{Area of the combined shapes}=\amp \text{area of all the three figures calculated} \\
=\amp 280cm^2 +126cm^2+77cm^2 \\
=\amp 483cm^2
\end{align*}
\(Alternatively:\) add up the area of the trapezium and the semicircle.
\begin{align*}
\text{Area of the trapezium}=\amp \frac{1}{2} h(a+b) \\
=\amp \frac{1}{2} \times 14(20+18+20) \\
= \amp 7cm \times 58cm \\
= \amp406cm^2
\end{align*}
Area of the semi circle \(=77cm^2\)
\begin{align*}
\text{Area of the combined shape} =\amp \text{Area of the two figure} \\
= \amp 406cm^2+77cm^2 \\
=\amp 483cm^2
\end{align*}
