Skip to main content
Contents Dark Mode Prev Up Next \(\newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\R}{\mathbb R}
\newcommand{\lt}{<}
\newcommand{\gt}{>}
\newcommand{\amp}{&}
\definecolor{fillinmathshade}{gray}{0.9}
\newcommand{\fillinmath}[1]{\mathchoice{\colorbox{fillinmathshade}{$\displaystyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\textstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptscriptstyle\phantom{\,#1\,}$}}}
\)
Section 3.4 Volume and Capacity
\({\color{Magenta} \text{Need for learning volume and capacity.}}\)
Did you take tea in the morning? Was it packed and labelled e.g 1 litre or 500ml? Now let’s explore to understand why we learn volume and capacity. The Importance of Volume and Capacity in the Milk Industry. The milk industry relies heavily on volume and capacity calculations at every stage—from production and storage to packaging and distribution. Understanding these concepts ensures efficiency, accuracy, and cost-effectiveness in the industry.
Subsection 3.4.1 Cubic metre as a unit of measuring volume
Activity 3.4.1 .
\(\displaystyle \textbf{What you need:}\)
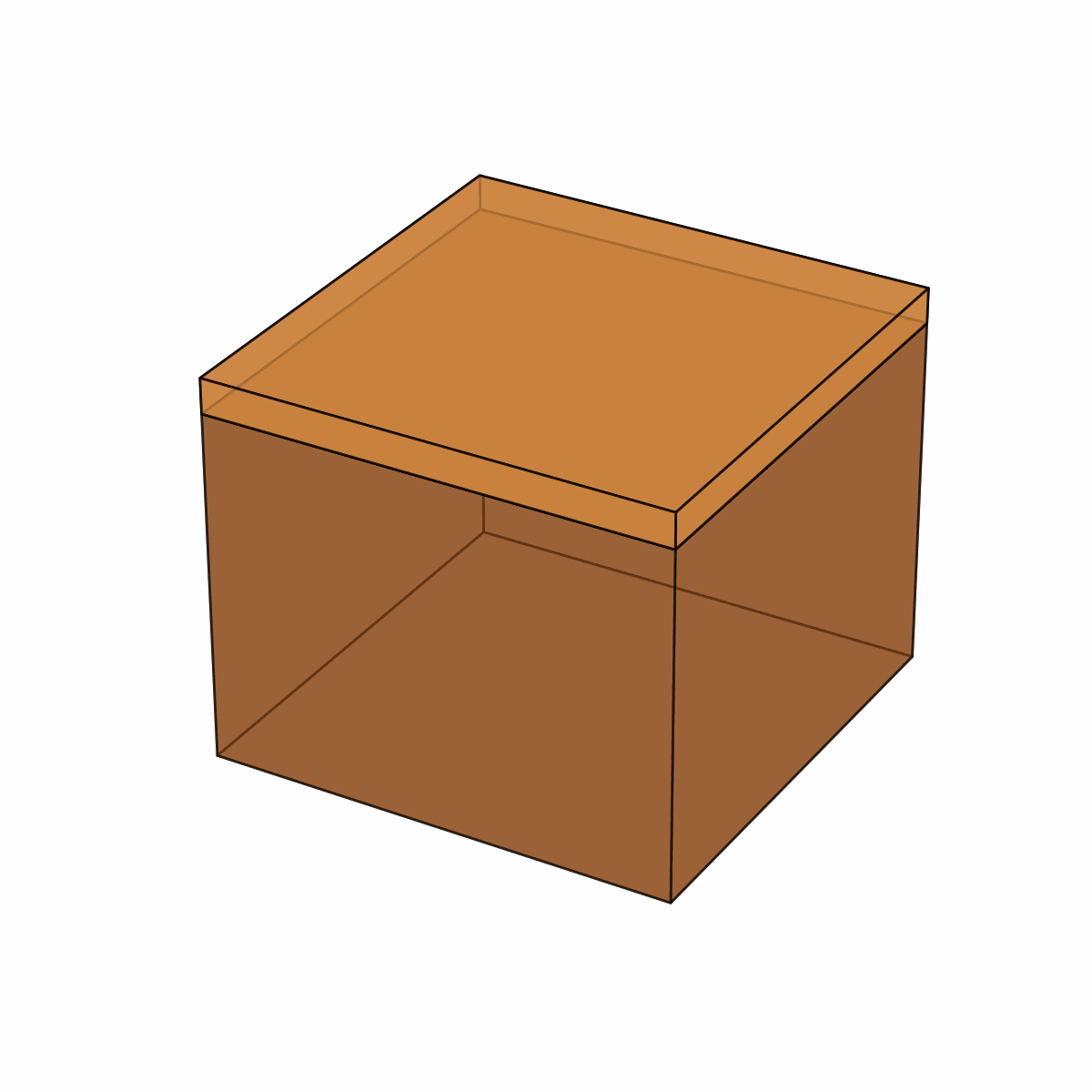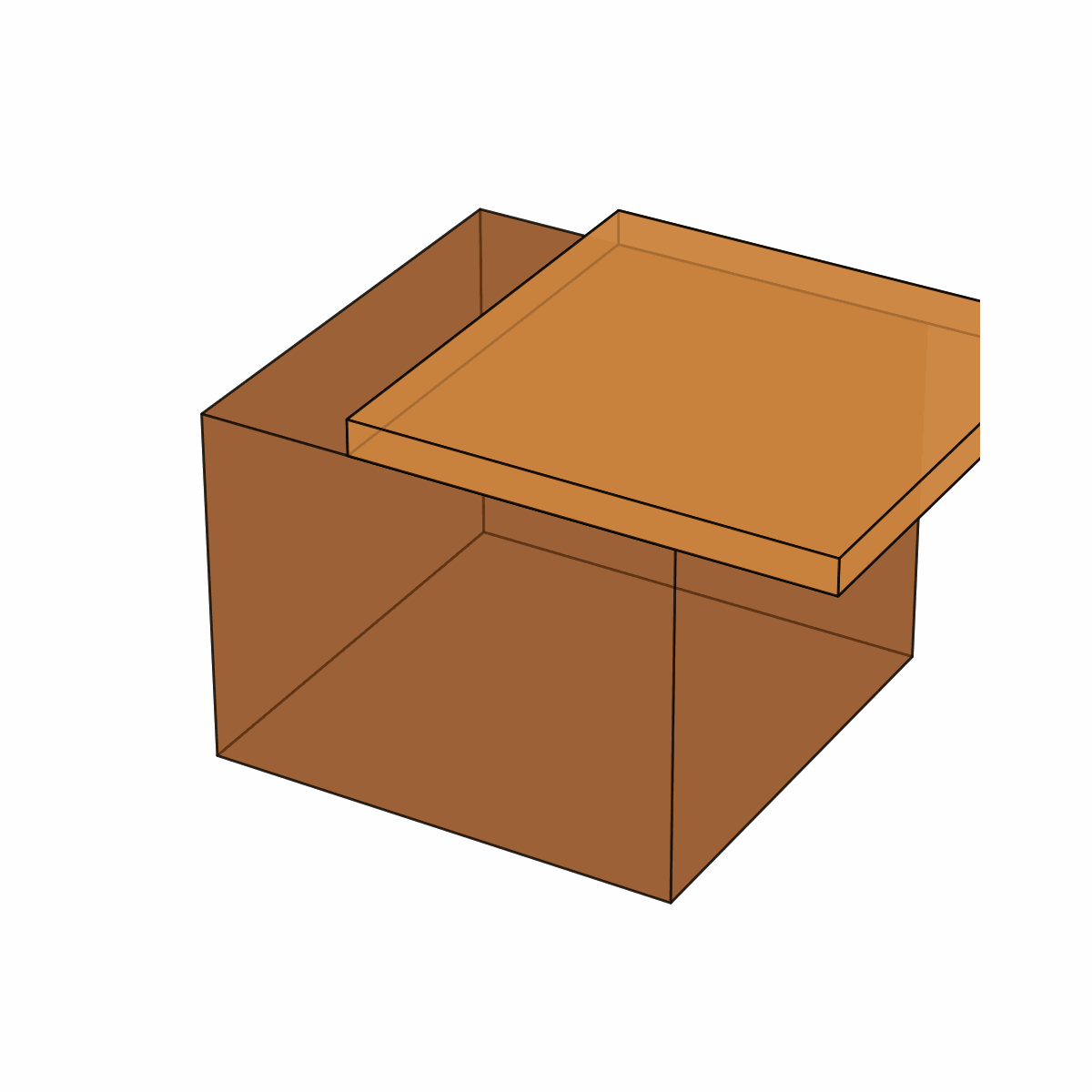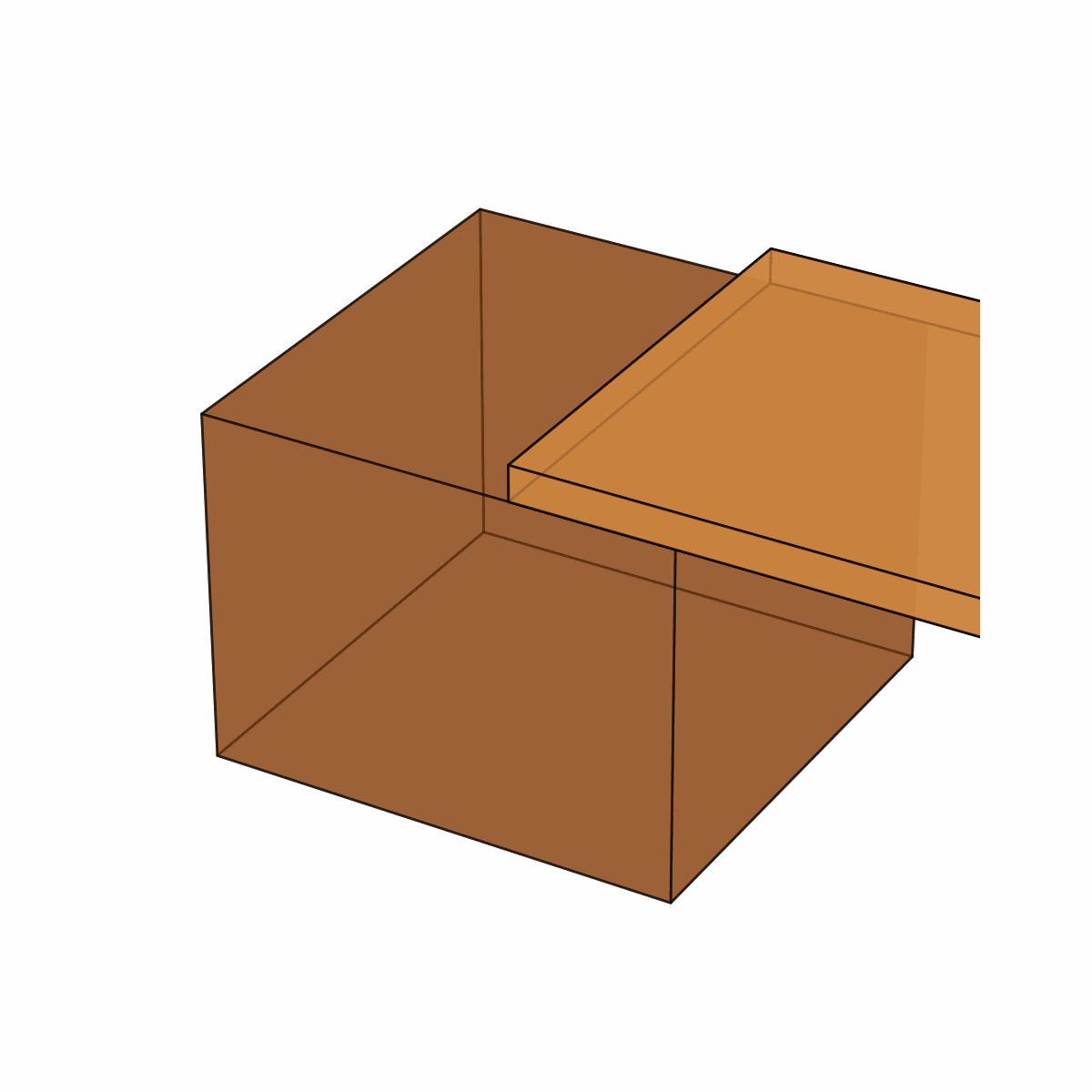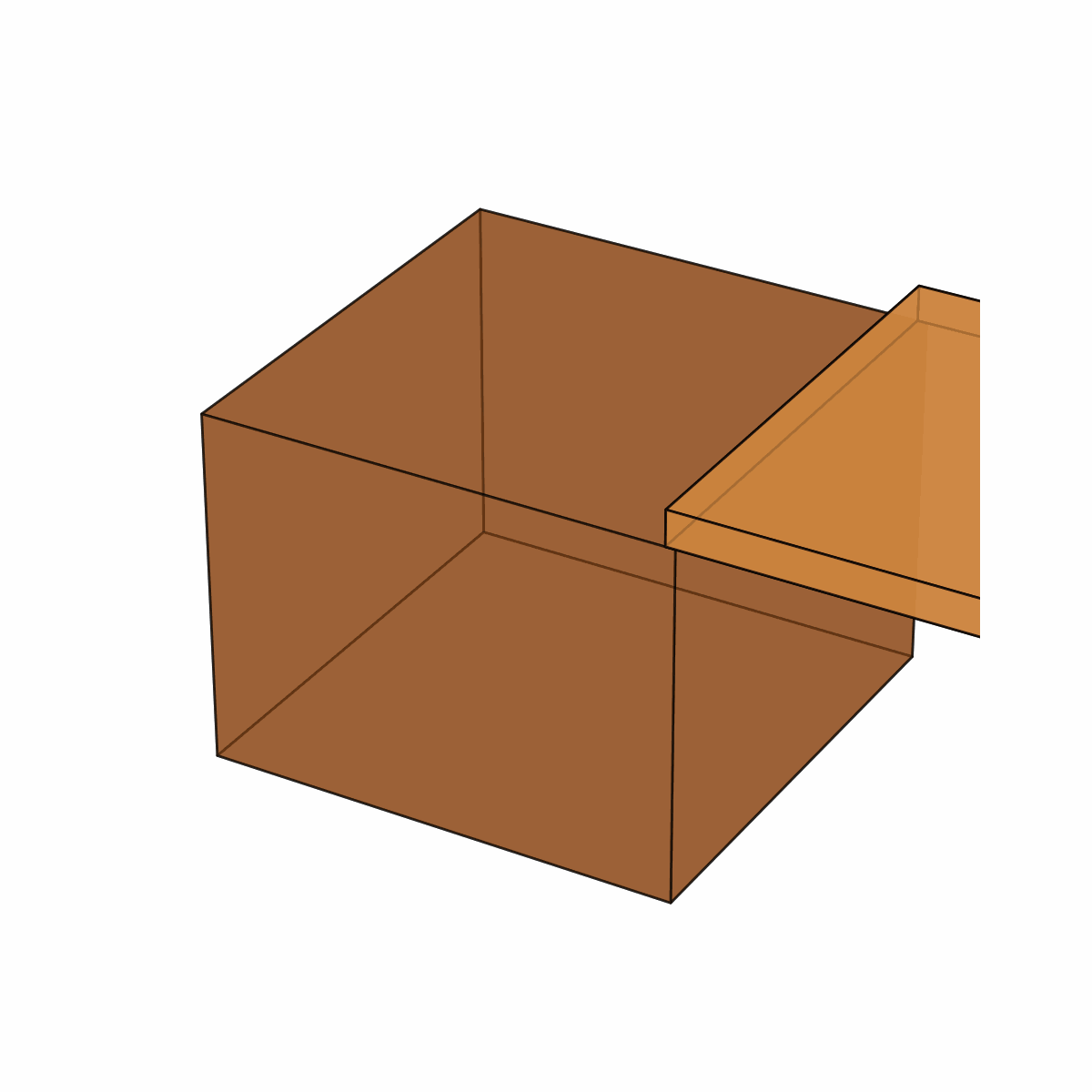
Cut six pieces square shaped with equal length of 30cm wide and long. Mount them together to form a cube as shown alongside. use the cut pieces of box to cover it all around to make a closed cube.
what is the volume of the cube you have made?
The cube you have made is called a
\({\color{Magenta} \text{20cm cube.}}\text{.}\) It’s sides are
\(20\text{cm}\) long.
The volume of the cube is
\(20\text{cm} \times 20\text{cm} \times 20\text{cm} = 1\text{cm}^3\)
\({\color{Magenta} \text{Conversion of cubic metres to cubic centimetres.}}\)
Suppose you have a cube with the length, the width and the height of 1 metre. Work out it’s volume in cubic metres.
\(1\text{m} \times 1\text{m} \times 1\text{m} = 1\text{m}^3\)
Measure the length, the width and the height of the cube in centimetres. Work out it’s volume in cubic centimetres.
\(100\text{cm} \times 100\text{cm} \times 100\text{cm} = 1,000,000\text{cm}^3\)
How many cubic centimetres is one cubic metre?
\(1,000,000\text{cm}^3\) How can you convert the volume you got in cubic metres to cubic centimetres? Since
\(1\text{m}^3 = 1,000,000\text{cm}^3\)
Therefore to convert volume from cubic metres to cubic centimetres, we multiply the volume by 1,000,000.
Example 3.4.1 .
A Rectangular tank has a volume of
\(\text{12m}^3.\) What is it’s volume in cubic centimetres?
\({\color{magenta}\text {Solution:}}\)
\begin{align*}
1 \text{m}^3= \amp 1000000\text{cm}^3 \\
12 \text{m}^3= \amp ? \\
\frac {12 \cancel{{m}^3}}{1\cancel{\text{m}^3}}\times 1000000 \text{cm}^3 = \amp 12 \times 1000000 \text{cm}^3 \\
=\amp 12,000,000\text{cm}^3
\end{align*}
Subsection 3.4.2 Volume of cubes.
Activity 3.4.2 .
Grade 7 learners intended to purchase a gift for their mathematics teacher.
Make a cubic gift box like the one shown below and measure the length, width and height to get it’s volume.
Thereafter, sketch the cube in your exercise book and work out the volume and convert the volume from
\(cm^3\) to
\(m^3.\)
What is the area of the coloured face?
Therefore find the area of the cube.
Example 3.4.2 .
Find the volume of the figure below.
Hint .
Volume of a cube =
\(l \times l \times l = l^3\)
Solution .
\begin{align*}
\text{Volume of a cube} = \amp {l} \times {l} \times {l} \\
=\amp {l} ^3\\
=\amp 3\text {m} \times 3\text{m} \times 3 \text{m}\\
=\amp 3^3\text({m}^3) \\
=\amp9\text{m}^3
\end{align*}
\({\color{Magenta}\text{Volume of the cube} = 9 \text{m}^3}\)
Subsection 3.4.3 volume of cuboids
Activity 3.4.3 .
Baya drew the cuboid alongside and coloured it at one face.
What is the area of the coloured face?
What is the volume of the cuboid?
Example 3.4.3 .
Find the volume of the figure below.
Hint .
Volume of the cuboid
\(= \text {length} \times \text{width} \times \text {height}.\)
Solution .
\begin{align*}
\text{volume of a cuboid} = \amp \text {length} \times \text {width} \times \text{height}\\
= \amp (12 \times 4 \times 5) \text{cm}\\
= \amp 240 \text{cm}^3
\end{align*}
\({\color{Magenta}\text{Volume of the cuboid} = 240 \text{cm}^3}\)
Subsection 3.4.4 Volume of cylinders
Activity 3.4.4 .
Arrange a pile of similar coins or round objects to form a cylinder as shown alongside.
Measure the diameter of the coin at the top.
Find the area of the coin{cross sectional area of the cylinder.}
Using a ruler, measure the height of the pile.
Multiply the height of the pile by the cross sectional area.
Share your answer with other learners.
Exploration 3.4.5 .
What is meant by cross section?
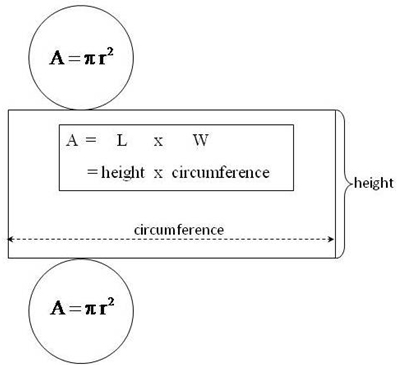
\(\text {Cross- sectional area } \textbf{A = π × r² = πr²}.\)
\(\text{volume of a cylinder} \textbf{ V =cross sectional area × height = πr²h}.\)
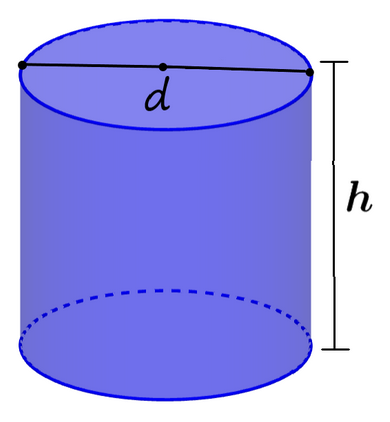
In the figure provided below adjust the height and radius of the cylinder by dragging the blue circle.
Figure 3.4.4. Volume of a cylinder.
Example 3.4.5 .
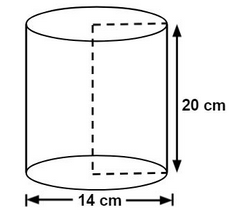
Find the volume of the cylinder alongside given d =
\(28\text{cm}\) and h =
\(50\text {cm}\)
Hint .
volume =
\(\pi \text {r}^2 \text {h}\)
Where d =
\(\frac {1}{2}\) r
Solution .
\begin{align*}
\text {Volume of a cylinder} =\amp \pi r^2 \\
=\amp \frac {22}{7} \times {14}{2}\text {cm}\times 14 \text {cm}\times 20 \text {cm} \\
=\amp \frac{22}{7} \times 3920 \text {cm}^2 \\
=\amp 12,320 \text {cm}^3
\end{align*}
Subsection 3.4.5 Relationship between cubic centimetres(cm³), cubic metres(m³) and Litres
Activity 3.4.6 .
\(\displaystyle \textbf {You need:} \)
\(\displaystyle {\color{Cyan} a).\text{A container. b)A basin.}}\)
\(\displaystyle {\color{Cyan}\text{ c) Water. d)A wood saw.}}\)
\(\displaystyle {\color{Cyan}\text {e)A piece of wood. f) A nail.}}\)
\(\displaystyle {\color{cyan} \text {h)A measuring cylinder calibrated in litres.}}\)
Make a model of a cube or (cut a cubic piece of wood) measuring
\(10 \text {cm by }10 \text {cm by }10 \text {cm}\text{.}\)
What is the volume of the cube?
Fill in the container with water and place it in the basin.
Hammer a nail on the cube.
Slowly immerse the cube into the water in the container until it is completely covered bt the water.
Pour the water that spilled into the water in a measuring cylinder and record the volume of the water.
\begin{gather*}
\textbf {a. What is the volume of the water that spilled?} \\
\textbf {b.What is the volume of the cube?}
\end{gather*}
Exploration 3.4.7 .
\({\color{magenta} \text{Learning point.}}\)
\({\color{cyan}\textbf {Conversion from cubic centimetres to Litres }}\)
From our activity above, The volume of water spilled should be \(1\) litre. The amount of water spilled in the basin is equivalent to the volume of the cube.
\begin{align*}
10 \text{cm} \times 10 \text{cm} \times 10 \text {cm} =\amp 1000\text {cm}^3\\
1000\text {cm}^3 =\amp 1 \text{Litre}\\
1 \text{Litre} = \amp 1000\text {cm}^3
\end{align*}
Activity 3.4.8 .
Learners from Kigali primary school used a 10 litre jerrycan to fill a
\(1 \text{m}\) cube container with water.
What is the volume of a
\(1 \text{m}\) cube container?
How many
\(10 \text{Litres}\) container filled the
\(1 \text{m}\) cube?
Share your findings with other class members.
Exploration 3.4.9 .
\({\color{green}\text {A hundred 10 Litres containers were used to fill the 1 m cube container.}}\)
\begin{align*}
100 \times 10 \text{litres} = \amp 1000 \text {Litres} \\
1000 \text {Litres} = \amp 1\ text{m}^3 \\
1 \text {m}^3 = \amp 1000 \text {Litres}
\end{align*}
Fill in the tables below to show relationship between
\(\text {cm}^3\text{,}\) \(\text {m}^3\) and
\(\text {Litres}\) .
Table 3.4.6. Relating \(\text {cm}^3\text{,}\) \(\text {m}^3\) and \(\text {Litres.}\)
\(\text {m}^3\) \(\text {Litres}\) \(\text {cm}^3\)
1 \(\text {m}^3\)
Table 3.4.7. Relating \(\text {cm}^3\) and \(\text {Litres.}\)
\(\text {Litres}\) \(\text {cm}^3\)
\(1 \text {litres}\)
Subsection 3.4.6 Relating volume to capacity.
Activity 3.4.10 .
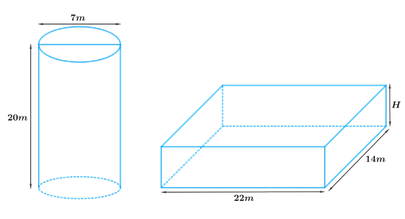
Mohono a grade 7 learner, drew the shapes below in his laptop where
\(\text{H} = 7\text{cm}\text{.}\)
Find the capacity of each shape He drew in litres.
\({\color{cyan} \text{Hint:} } 1 \text{m}^3 = 1000\text {Litres}\)
Example 3.4.8 .
Find the capacity of the cylinder alongside in Litres.
Solution .
Find the volume of the cylinder.
\begin{align*}
\text{Volume of the cylinder } =\amp \pi \text{r}^2\text{h}\\
=\amp \frac{22}{7}\times 7\text{cm} \times 7\text{cm} \times 20\text{cm}\\
=\amp \frac{22}{7} \times 980\text{cm}^2\\
=\amp 3,080\text{cm}^3
\end{align*}
Convert \(3,080\text{cm}^3\) into Litres.
\begin{align*}
1000\text{cm}^3 =\amp 1 \text{Litre}\\
3,080\text{cm}^3 =\amp (3,080 \div 1000) \text{Litres}\\
=\amp 3.08 \text{Litres}
\end{align*}
\({\color{green}\text {The capacity of the cylinder is } 3.08 \text { Litres. }}\)