Skip to main content

Grade 7 Mathematics Learner’s Book

INNODEMS

Section 3.5 Time,Distance and speed

Subsection 3.5.1 Time,Distance and speed

Why time, distance and speed.
🔗
  • We use time, distance and speed in our daily life.
    🔗
    🔗
  • Time helps us to plan our day-to-day activities.Knowing distance helps us to plan when emberking on a journey. Speed helps us to determine how long we would take to cover a certain distance.
    🔗
    🔗
🔗
Time
Note:
🔗
time
  • Time is measured in seconds, minuites and hours.
    🔗
    Therefore, \(hours\text{,}\) \(minutes\) and \(seconds\) are the units of measurering time.
    🔗
    🔗
🔗

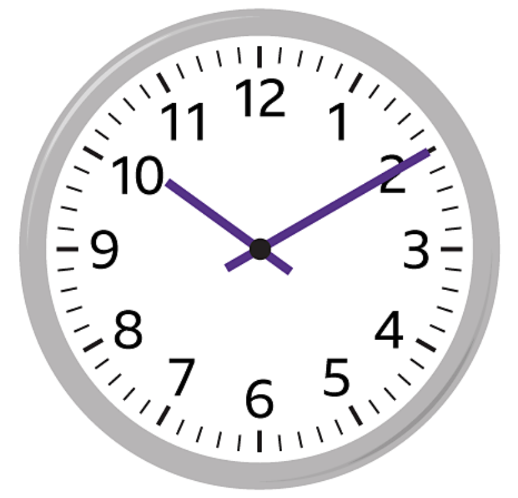
Example 3.5.1.

What is the time on the clock face below?
🔗
Solution.
The hour hand points at \(10\text{.}\) The minute hand point at \(2\text{.}\)
🔗
The time is \(10:10\)
🔗
🔗
🔗

Example 3.5.2.

Moraa recorded the time she spent during a morning run exercise.
🔗
Exe2
For how long did he run?
🔗
Solution.
Moraa ran for \(2\, hour \,14 \,minuites \, 22 \, seconds\text{.}\)
🔗
🔗
🔗
🔗

Subsection 3.5.2 Units of measuring time

Units of mesurering time are;
🔗
  1. Minutes
    🔗
    🔗
  2. Hours
    🔗
    🔗
  3. Seconds
    🔗
    🔗
🔗

Subsubsection 3.5.2.1 Converting hours to minutes

\(1\) hour \(=\) \(60\) minutes.
🔗
Activity 3.5.1.
Work in pairs.
🔗
  1. Whate you need.
    🔗
    razer blade,manniler paper(white and yellow), black maker pen,a wire and a pair of campus.
    🔗
    🔗
  2. Make a clock face like the one shown alongside using a paper cut out.
    🔗
  3. Move the minute hand clockwise to make a complete turn.
    🔗
  4. How many minutes does the minuite hand cover in one complete turn?
    🔗
  5. Observe how the hour hand moves when the minute hand make one complete turn. What have you noticed?
    🔗
  6. Share your findings with other learners in class.
    🔗
🔗
Clock
Learning point.
🔗
From the above activity you should notice that;
🔗
\(1\) hour \(=\) \(60\) minutes.
🔗
🔗
Example 3.5.3.
Convert \(3\) hours
🔗
Hint.
Conversion of hours to minutes, we use the conversion units that is \(1 \, hour \,= \,60 \,minuites \text{.}\)
🔗
🔗
Solution.
\begin{align*} 1 \, hour =\amp 60 \, minutes\\ 3 \, hours =\amp (3 \times 60)\, minutes \\ =\amp 180 \, minutes \end{align*}
🔗
Therefore,
🔗
\(3\, hours = 180 \, minutes\)
🔗
🔗
🔗
Example 3.5.4.
How many minuites are the in \(3\frac{1}{2}\) hours?
🔗
Solution.
\(1 \, hour = 60 \, minutes\)
🔗
\begin{align*} 3\frac{1}{2}\,hours=\amp (3\frac{1}{2} \times 60) \, minutes\\ =\amp (\frac{7}{2} \times 60) \, minutes\\ =\amp \frac{420}{2} \,minuites\\ =\amp 210 \, minutes \end{align*}
🔗
Therefore,
🔗
\(3\frac{1}{2}\,hours= 210 \, minutes \)
🔗
🔗
🔗
Example 3.5.5.
A motorist took \(8 \, hours \) to travel from Kilifi to Machakos. How many minutes did he take during the travel?
🔗
Solution.
Hours he took was \(8 \, hours\)
🔗
To convert the hours taken to minuites, use \(1 \, hour=60 \, minutes\)
🔗
Therefore,
🔗
\begin{align*} 8 \, hours=\amp(8 \times 60)minutes \\ =\amp 480\, minutes \end{align*}
🔗
The minutes taken for the travel is \(480\, minutes\)
🔗
🔗
🔗
🔗

Subsubsection 3.5.2.2 Converting minutes into hours

As discused before that \(1\,hour=60 \, minutes\text{.}\) it’s clear to see also that \(60 \, minutes=1\,hour\text{.}\)
🔗
Activity 3.5.2.
Work in groups.
🔗
  1. Grade 7 learners recorded the time they spent doing various activities during their leisure time.
    🔗
    Name Activity Time taken in minutes Time taken in hours
    Moraa Running 120
    Akinyi Playing football 90
    Ekadeli Reading story books 60
    🔗
  2. Why should we engage in positive leisure activity?
    🔗
  3. Fill in the table to show the time spent by each learner in hours.
    🔗
  4. Share your work with other learners in class.
    🔗
🔗
🔗
Example 3.5.6.
A bus took \(560 \, minutes \) to travel from Kisumu to Nairobi. What time did it take in hours and minutes?
🔗
Solution.
The bus took \(560\, minutes\)
🔗
Note that, \(60 \, minutes=1\,hour\)
🔗
\begin{align*} 560 \, minutes=\amp (560 \div 60)hours\\ =\amp 9 \, hours \, 20 \, minutes \\ \amp \end{align*}
🔗
9 hours
60 560
-540
20 mins
The bus took \(9 \, hours \, 20 \, minutes\) to travel from Kisumu to Nairobi.
🔗
🔗
🔗
🔗

Subsubsection 3.5.2.3 Converting minutes into seconds

The statment for conversion states that,
🔗
\(1 \, minute \,= 60 \, seconds\text{.}\)
🔗
Activity 3.5.3.
  1. Using a stopwatch or a rist watch or a clock watch, observe and record the number of seconds in the following minutes.
    🔗
    Minutes Seconds
    1 minute
    3 minutes
    5 minutes
    10 minutes
    🔗
  2. How many seconds are there in a minutes?
    🔗
  3. Share your findings with other learners in class.
    🔗
🔗
🔗
Example 3.5.7.
a).Convert \(12 \, minutes \) into seconds.
🔗
b). Owilii took \(5 \, minutes \,24 \, seconds\) to walk from the classroom to the school gate. How nuch time did she take in seconds to reach the school gate?
🔗
Solution.
a).
🔗
\begin{align*} 1 \, minute=\amp 60 \ seconds \\ 12 \, minutes= \amp 12 \times 60 \, seconds \\ =\amp 720 \, seconds\\ \text{Therefor,} \, 12 \, minutes=\amp 720 \, seconds \end{align*}
🔗
b).
🔗
\begin{align*} 1 \, minutes= \amp 60 \,seconds \\ 5 \, minutes \, 24 \, seconds=\amp 5 \, minutes+ 24 \, seconds\\ =\amp (5 \times 60)\, seconds + 24 \, seconds \\ =\amp 300 \, seconds + 24 \, seconds \\ =\amp 324 \, seconds \end{align*}
🔗
🔗
🔗
🔗

Subsubsection 3.5.2.4 Converting second into minutes.

Converting seconds into minutes depend on the previous sub-topic.
🔗
Notice that, \(60 \, seconds = 1 \,minutes\)
🔗
Activity 3.5.4.
  1. Using a stopwatch or a rist watch or a clock watch, observe and record the number of minutes in the following seconds.
    🔗
    Seconds Minutes
    60 seconds
    120 seconds
    180 seconds
    240 seconds
    300 seconds
    🔗
  2. Share your work with other learners in class.
    🔗
🔗
🔗
Example 3.5.8.
A digital game took \(200 \, seconds\text{.}\) How long did the digital game take in munites and seconds?
🔗
Solution.
\begin{align*} 60 \, seconds=\amp 1 \, minutes \\ 200 \, seconds=\amp (200 \div 60) \, minutes \\ =\amp 3 \, munites 20 \, seconds \end{align*}
🔗
3 minutes
60 200
-180
20 seconds
Therefore,
🔗
The digital game took \(3 \, minutes \, 20 \, seconds\)
🔗
🔗
🔗
🔗

Subsubsection 3.5.2.5 Converting hours into seconds

By the conversion above for minutes to hours,seconds to minutes,etc,
🔗
Convertion of hours to second, use \(1 \, hour =3600 \,seconds\text{.}\)
🔗
Example 3.5.9.
Convert \(7 \, hours \) to seconds.
🔗
Solution.
if \(1 \, hour = 3\,600 \, seconds\text{,}\) Therefore,
🔗
\begin{align*} 7 \, hours= \amp (7 \times 3\,600)\,seconds \\ =\amp 25\,200 \, seconds \end{align*}
🔗
\(7 \, hours= 25\,200 \, seconds\)
🔗
🔗
🔗
Example 3.5.10.
Morara covered a certain distance in \(2 \, hours\text{.}\) How long did the journey take in seconds?
🔗
Solution.
If \(1 \, hour = 3\,600 \, seconds\text{,}\) therefore,
🔗
\begin{align*} 2 \, hours = \amp (2 \times 3\,600) \, seconds \\ =\amp 7\,200 \, seconds \end{align*}
🔗
The journey took \(7\,200 \, seconds\text{.}\)
🔗
🔗
🔗
🔗

Subsubsection 3.5.2.6 Converting second into hours

As stated earlier that, \(1 \, hour = 3\,600 \, seconds\)
🔗
It also implies that, \(3\,600 \, seconds= 1 \, hour\text{.}\)
🔗
Activity 3.5.5.
Work in groups of 4
🔗
  1. Fill in the table below. You may use a calculator to work out the division.
    🔗
    Seconds Minutes Hours
    \(3\,600\) \(60\)
    \(7\,200\)
    \(10\,800\)
    \(14\,400\)
    🔗
  2. Share your answer with other learners in your class.
    🔗
    🔗
🔗
🔗
Example 3.5.11.
Convert \(10\,800 \, seconds\) into hours.
🔗
Solution.
If \(3\,600 \, sedconds = 1\,hour\)
🔗
\begin{align*} 10\,800 \, seconds= \amp (10\,800 \div 3\, 600) hours \\ = \amp 3\, hours \end{align*}
🔗
\(10\,800 \, seconds = 3 \, hours\text{.}\)
🔗
🔗
🔗
Example 3.5.12.
Baya spent \(7\,200 \, seconds \) seconds washing clothes. How much time did he spend in hours?
🔗
Solution.
\begin{align*} 3\,600 \, seconds=\amp 1 \, hour \\ 7\,200 \, seconds =\amp (7 \, 200 \div 3\, 600)\, hours\\ = \amp 2 \, hours \end{align*}
🔗
Therefore,
🔗
Baya spent \(2 \, hours\) washing clothes.
🔗
🔗
🔗
🔗
🔗

Subsection 3.5.3 Units of measuring distance.

Distance is the length of the space between two points. eg
🔗
Distance from the grade 7 classroom and the assembly, home to school, assembly to your school latrine and etc.
🔗
The SI unit of measuring distance is \(kilometres \, \text{and} \, metres\text{.}\)
🔗
  • Kilometres can be written as \(km\text{.}\)
    🔗
    🔗
  • Metres can also be written \(m\text{.}\)
    🔗
    🔗
🔗

Subsubsection 3.5.3.1 Converting kilometres into metres

The conversions are as follows;
🔗
\(1\, kilometre= 1\,000 \, metres\)
🔗
Similarly \(1\,000 \, metres = 1\, kilometre\)
🔗
Activity 3.5.6.
  1. The distance from Jerald’s home to the school is \(3\,km\text{.}\) He walks to school and back every day. How many metres does he walk every day?
    🔗
    🔗
  2. Estimate the following distances in kilommetres and convert the estimated distance to metres.
    🔗
    Description Estimated distance in kilometres Estimated distance in metres
    a) The distance from the school to the nearest shopping centure.
    b) The distance from the classroom to the assembly ground.
    c) The distance from the school to the nearest police station.
    🔗
  3. Share your work with other learners in your class.
    🔗
    🔗
🔗
🔗
Example 3.5.13.
Convert \(12\,km\) to metres.
🔗
Solution.
If \(1 \, kilometre = 1\,000 \, metres\)
🔗
Therefore,
🔗
\begin{align*} 12 \, km = \amp (12 \times 1\,000)\, metres \\ =\amp 12\,000 \, metres \end{align*}
🔗
Therefore, \(12 \, km= 12\,000 metres\)
🔗
🔗
🔗
Example 3.5.14.
Josphat cycled for \(6.4 \, km\text{.}\) How many metres did he cycle?
🔗
Solution.
\begin{align*} 1\, km=\amp 1\,000 \,m \\ 6.4 \, km=\amp 6.4 \times 1 \, 000 \, m \\ =\amp 6\, 400 \,m \end{align*}
🔗
Josephat cycled for \(6\, 400 \, metres\text{.}\)
🔗
🔗
🔗
Example 3.5.15.
The distance from Owilli’s home to school is \(4\frac{1}{2} \, km\text{.}\) How many metres is the school away from Owili’s home?
🔗
Solution.
\begin{align*} 1\,km=\amp 1\,000 \, m \\ 4\frac{1}{2} \,km=\amp 4\frac{1}{2} \times 1\,000\, m \\ =\amp \frac{9}{2} \times 1\,000 \,m\\ =\amp \frac{9\,000}{2}\,m \\ = \amp 4\,500 \,m \end{align*}
🔗
The distance from Owili’s home to the school is \(4\,500 \,m\text{.}\)
🔗
🔗
🔗
🔗

Subsubsection 3.5.3.2 Converting metres to kilometres.

As discussed above, the conversion of metres to kilometres is, \(1\,000 \, metres= 1\, kilometre\)
🔗
Activity 3.5.7.
Work in groups.
🔗
  1. Grade 7 learners made the number cards below.
    🔗
    \(1\,000\,m\)
    \(3\,000\,m\)
    \(4\,000\,m\)
    \(10\,000\,m\)
    🔗
  2. Convert each of the above distance into kilometres
    🔗
    Hint: \(1\,000\,m=1\,km\text{.}\)
    🔗
    🔗
  3. Share your work with other learners in class.
    🔗
    🔗
🔗
🔗
Example 3.5.16.
Convert \(17\,000\, m\) to kilometres.
🔗
Solution.
Using the conversion formula that outlines, \(1\,000\,m=1\,km\text{.}\)
🔗
\begin{align*} 1\,000 \, m=\amp 1 km \\ 17\,000m=\amp (17\, 000 \div 1\, 000)\,km \\ =\amp 17\, km \end{align*}
🔗
Therefore,
🔗
\(17\,000\,m= 17 \, km\)
🔗
🔗
🔗
Example 3.5.17.
During a sports day, Murunga ran a distance of \(3\, 700\,m\text{.}\) What distance did he cover in kilometres?
🔗
Solution.
\begin{align*} 1\, 000\, m=\amp 1\,km \\ 3 \, 700\,m =\amp (3\, 700 \div 1\, 000)\, km \\ =\amp (\frac{3\,700}{1\,000})\, km \\ =\amp 3.7 \,km \end{align*}
🔗
Murunga coverd \(3.7 \,km\text{.}\)
🔗
🔗
🔗
🔗
🔗

Subsection 3.5.4 Speed

Speed - is the total distance covered over the time taken in any activity done.
🔗
The SI unit of measuring speed is kilometres per hour(\(km/h\)) or metres per second(\(m/s\)).
🔗

Subsubsection 3.5.4.1 Speed in kilometres per hour (km/h).

Speed is measured in \(km/h\text{.}\)
🔗
Activity 3.5.8.
Work in groups
🔗
Go outside the classroom to the school’s athletics field.
🔗
  1. Take a walk outside the classroom and go to an athletics field.
    🔗
    One lap on the athletic field is \(400\,m \, (0.4)\,km\)
    🔗
    🔗
  2. Walk round the field one lap and record the time you take.
    🔗
    🔗
  3. Run round the field once and record the time you take.
    🔗
    🔗
  4. Run round the field two times and record the time you take.
    🔗
    🔗
  5. Run round the field three times and record the time you take.
    🔗
    🔗
  6. Fill the table below.
    🔗
    Description Distance in \(km\) Time taken in hours \(speed = \frac{distance}{time}\)
    a) Walking round the field once \(0.4\,km\)
    b) Running round the field \(0.4\,km\)
    c) Running round the field twice \(0.8\,km\)
    d) Running round the field thrice \(1.2\,km\)
    🔗
  7. Share your work with other learners in your class.
    🔗
    🔗
🔗
Figure 3.5.18. Perimeter of different plane figures.
🔗
LEARNING POINT
🔗
  • Speed is expressed in terms of distance covered per unit time.
    🔗
    🔗
  • \(\displaystyle Speed= \frac{distance}{time \, taken}\)
    🔗
  • Speed can either be expressed in kilometres per hour (\(km/hr\)) or metres per second (\(m/s\)).
    🔗
🔗
🔗
Example 3.5.19.
A truck travelled a distance of \(240 \, km\) in \(4\, hours\text{.}\) What was its speed in kilometres per hour?
🔗
Solution.
\begin{align*} speed= \frac{distance}{time} \amp \\ Distance \,covered=\amp 240 \, km \\ Time \,taken= \amp 4 \, hours \\ Speed=\amp \frac{240 \, km}{4\, hours} \\ =\amp 60 \, km/h \end{align*}
🔗
The speed for the truck is, \(60 \, km/h\text{.}\)
🔗
🔗
🔗
Example 3.5.20.
Akinyi walked a distance of \(25\, kilometres\) in \(5 \, hours\text{.}\) What was her speed in \(km/h\)
🔗
Solution.
\begin{align*} speed=\amp \frac{distance}{time} \\ Distance \, covered=\amp 25 \, km \\ Time \, taken=\amp 5 \, hours \\ Speed= \amp \frac{25 \, km}{5 \, hours} \\ =\amp 5 \, km/h \end{align*}
🔗
Her speed was \(5 \, km/h\)
🔗
🔗
🔗
🔗

Subsubsection 3.5.4.2 Speed in metres per-second(m/s)

Speed can also be expressed in metres per second(\(m/s\)).
🔗
Activity 3.5.9.
Work in groups
🔗
  1. Take a walk outside the classroom.
    🔗
    🔗
  2. Mark a distancde of \(100\, m\) in the field.
    🔗
  3. Take turns to run the \(100\, m\) .
    🔗
  4. Use a stopwatch to record the time taken by each learner in the group
    🔗
  5. Fill in the table below.
    🔗
    Name of the learner Distance in metres Time taken in sedconds \(speed= \frac{distance}{time}\)
    a) \(100 \, m\)
    b) \(100 \, m\)
    c) \(100 \, m\)
    🔗
  6. Share your work with other learners in your class.
    🔗
    🔗
🔗
🔗
Example 3.5.21.
Mark covered a distance of \(100\,m\) in \(20\, seconds\text{.}\) What was his speed in metres per seconds?
🔗
\(Speed = \frac{distance \, covered}{time \, taken}\)
🔗
Distance he covered \(=100\,m\text{,}\) Time he took \(20 \, seconds \)
🔗
Therefore,
🔗
\begin{align*} speed=\amp (100 \, m \div 20 \, seconds)\\ = \amp (\frac{100}{20}) \, m/s\\ = \amp 5 \, m/s \end{align*}
🔗
Mark’s speed is \(5 \, m/s \text{.}\)
🔗
🔗
Example 3.5.22.
A cyclist covered a distance of \(200\,m\) in \(2\, minutes \text{.}\) What was his speed in \(m/s\text{?}\)
🔗
Hint.
Convert \(2\, minutes \,to \,seconds \,\text{ by the conversion rule}\)
🔗
\(1 \, minutes= 60 \, seconds\)
🔗
🔗
Solution.
Converting \(2\, minutes\) to seconds
🔗
if
\begin{align*} 1 \, minutes=\amp 60 \, seconds \\ 2\, minutes= \amp 2\, minutes \times 60 \, seconds\\ = \amp 120\, seconds\\ \text{speeed}=\amp (\frac{1\,200}{120})\,m/s \\ = \amp 10 \,m/s \end{align*}
🔗
The speed for the cyclist was \({\color{blue} 10\,m/s}\)
🔗
🔗
🔗
🔗
🔗

Subsection 3.5.5 Converting units of speed.

Speed can be converted from kilometre per hour\((km/h)\) to metres per second\((m/s)\) and also metres per second\((m/s)\) to kilometre per hour\((km/h)\text{.}\)
🔗
Figure 3.5.23. Perimeter of different plane figures.
🔗

Subsubsection 3.5.5.1 Converting speed in kilometre per hour\((km/h)\) to metres per second\((m/s)\text{.}\)

\({\color{green} \text{Work in groups}}\)
🔗
Read the story below.
🔗
Juma is a school driver. He drives carfully and observes all the traffic rules. One day, he took learners for on educatianal trip. He drove at a speed of \(60\,km/hr\text{.}\)
🔗
  1. Why is it important to observe traffic rules?
    🔗
    🔗
  2. How many kilometres did the bus cover in \(1\) hour?
    🔗
  3. What was the speed of the bus in \(m/s\text{?}\)
    🔗
  4. Share your work with other learners in class.
    🔗
🔗
\({\color{blue} \text{Learning point.}}\)
🔗
To convert speed speed in kilometre per hour to metres per second, you convert the distance to metres and one hour to seconds, then devide.
🔗
Example 3.5.24.
A car travelled a distance of \(180\,km\) in \(2\) hours. What was the speed of the car in \(m/s\text{?}\)
🔗
Solution.
\begin{align*} \text{If} \, 1\,km= \amp 1\,000\,m \\ 180\,km=\amp 180 \times 1\,000\,m \\ =\amp {\color{green} 180\,000\,m}\\ \text{If} \,1\,hour=\amp 3\,600 \, seconds \\ 2\, hours=\amp 2 \times 3\,600 \, seconds \\ =\amp {\color{green} 7\,200\, seconds } \\ \text{Speed} =\amp \frac{Distance\,covered}{time\,taken} \\ =\amp (\frac{{\color{green} 180\,000}}{{\color{green} 7\,200}})\,m/s \\ =\amp {\color{blue} 25\,m/s} \end{align*}
🔗
a) Convert the distance from kilometres to metre.
b) Convert the time from hours to second.
c) Devide the distance in metres by the time in seconds.
🔗
🔗
🔗

Subsubsection 3.5.5.2 Converting speed in metres per second\((m/s)\) to kilometres per hour\(km/h\)

\({\color{green} \text{Work in groups}}\)
🔗
  1. The picture alongside shows an ambulence. The ambulence transported a sick person to Matibabu Hospital, \(72\,000\,m\) away.The journey took \(40\) minutes. Calculate the speed of the ambulence in metres per second.
    🔗
    🔗
  2. Work out the distance, in kilometres, that the ambulence coveredin one second.
    🔗
  3. How many kilometres did the ambulence cover in one hour?
    🔗
  4. What was the speed of the ambulence in kilometres per hour?
    🔗
  5. Share your work with other learners in class.
    🔗
🔗
\({\color{blue} \text{Learning point.}}\)
🔗
To convert speed in metres per second to kilometres per hour, you convert the distance to kilometres and the one second to hours, then divide.
🔗
Example 3.5.25.
In a swimming competition, the fastest swimmer took \(25\) second to complete a \(62.5\, m\) race. Calculate the speed of the swimmer in kilometres per hour
🔗
Solution.
First,
🔗
Convert \(62.5\, m\) to kilometres.
🔗
Convert \(25\, s\) to hours.
🔗
\begin{align*} \text{If} \,1\,000=\amp 1\,km\\ 62.5\,m=\amp \frac{62.5}{1\,000}\,km \\ =\amp \frac{1}{16}\,km\\ \text{If}\,3\,600\,s=\amp 1\,h \\ 25\,s =\amp \frac{25}{3\,600}\,h \\ \text{Speed} = \amp \text{distance} \div \text{time} \\ =\amp \frac{1}{16}\,km \div \frac{25}{3\,600}\,h \\ =\amp \frac{1}{16}\,km \times \frac{3\,600}{25}\,h\\ =\amp {\color{blue} 9\,km/h} \end{align*}
🔗
🔗
🔗
🔗
🔗
🔗
PrevTopNext