Skip to main content

Grade 7 Mathematics Learner’s Book

INNODEMS

Section 1.1 Whole Numbers

\(\textbf{Why study whole numbers? }\)
🔗
In our day to day-to-day lives, we use whole numbers to count objects i.e. Diera, a Grade 7 learner will use whole numbers to count her books. If one book is missing, she will notice this from the number of books she currently has.
🔗

Subsection 1.1.1 Place Value of digits in a number

Activity 1.1.1.

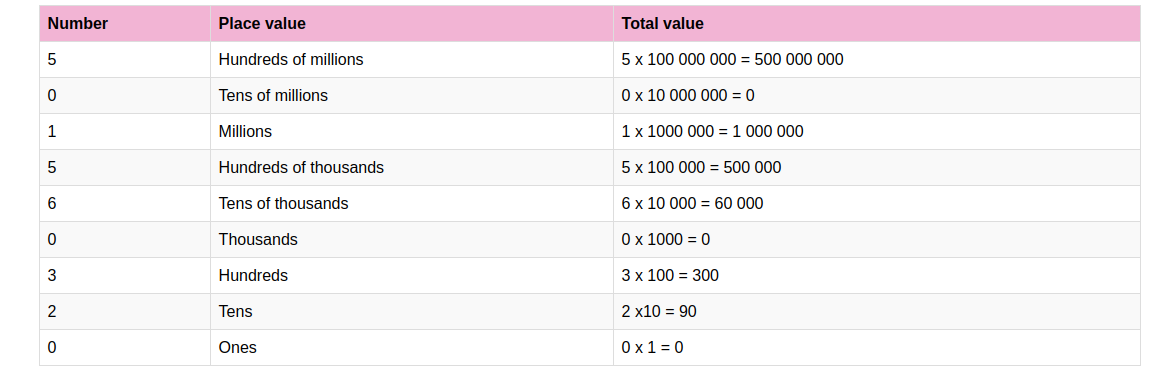
Pembe flour milling factory in Nairobi produced 85 147 000 kg of maize flour in the year 2023. In the year 2024, the factory produced 120 568 720 kg of maize flour.
🔗
1. Fill in the place values for the number of kilograms produced for the two years.
🔗
Table 1.1.1.
🔗
Numbers Hundreds of millions Tens of millions millions Hundreds of thousands Tens of thousands thousands Hundreds Tens Ones
\(85 147 000\)
\(120 588 720\)
2. Share your work with other learner’s in class.
🔗
🔗
\(\textbf{Online acitivity}\)
🔗
Click the link below to find more activities on place value of numbers.
🔗

Example 1.1.2.

In 2008, a county government allocated sh 501 560 320 towards the construction of a dam. Give the place value of digit 1 .
🔗
Solution.
To identify the place value of digit 1,use a place value chart as shown below.
🔗
Numbers Hundreds of millions Tens of millions millions Hundreds of thousands Tens of thousands thousands Hundreds Tens Ones
\(501 560 320\) 5 0 1 5 6 0 3 2 0
Therefore,
🔗
The place value of digit 0 is ones.
🔗
The place value of digit 2 is Tens.
🔗
The place value of digit 3 is Hundreds.
🔗
The place value of digit 0 is Thousands.
🔗
The place value of digit 6 is Tens of thousands.
🔗
The place value of digit 5 is Hundreds of thousands.
🔗
The place value of digit 1 is Millions.
🔗
The place value of digit 0 is Tens of millions.
🔗
The place value of digit 5 is Hundreds of millions.
🔗
🔗
🔗

Checkpoint 1.1.3.

🔗
🔗

Subsection 1.1.2 Total Value of digits in a number

The total value of a digit in a number is the product of the digit and its place value.
🔗

Activity 1.1.2.

  1. Make cards with numbers as shown below.
    🔗
    🔗
  2. Form a 9-digit number using the cards.
    🔗
    🔗
  3. Stick each card on a place value chart as shown below.
    🔗
    🔗
  4. Find the total value of each digit.
    🔗
    🔗
  5. Share your work with other learners in your class.
    🔗
    🔗
🔗
🔗

Example 1.1.4.

What is the total value of each digit in the number 501 560 320?
🔗
Solution.
The total value of a digit = digit x place value
🔗
Use a place value chart as shown below to find the total value of the digits in the number \(501 560 320\)
🔗
🔗
🔗

Example 1.1.5.

In 2005, 249 738 201 tree seedlings were planted in the country. What is the total value of digit 4 in the number of tree seedlings planted?
🔗
Solution.
The place value of digit 4 is tens of millions.
🔗
The total value of digit 4 is 4 x 10 000 000
🔗
The total value of digit 4 is 40 000 000.
🔗
🔗
🔗

Checkpoint 1.1.6.

🔗
🔗

Subsection 1.1.3 Reading and writing numbers in symbols

Activity 1.1.3.

(a) Consider the number 651 358 189.
🔗
(b) Make a place value chart as shown below.
🔗
Group Millions Thousands Units
Place value Hm Tm M HTh TTh Th H T O
Digit
(c) Insert the digits in the number \(651\, 358\, 189\) in their respective places in the place value chart.
🔗
(d)
  1. Read the number \(651\) in the group of millions i.e six hundred and fifty one million.
    🔗
    🔗
  2. Read the number \(358\) in the group of thousands i.e three hundred and fifty eight thousand.
    🔗
    🔗
  3. Read \(189\) in the group of hundreds and units i.e one hundred and eighty nine.
    🔗
    🔗
🔗
(e) Read the numbers in (d) continuously.
🔗
(f) Discuss and share how to read \(651\, 358\, 189\) with other groups.
🔗
🔗

Example 1.1.7.

Read and write five million, two hundred and thirty seven thousand, eight hundred and forty one in symbols.
🔗
Solution.
\(\text{ Five million }\) \(=\) \(5\,000\,000\)
\(\text{Two hundred and thirty seven thousand}\) \(=\) \(237\,000\)
\(\text{Eight hundred and forty one}\) \(=\) \(841\)
\(\text{Add the numbers}:5\,000,000 + 237\,000 + 841\) \(=\) \(5\,237\,841\)
🔗
🔗

Example 1.1.8.

Write the number one hundred and twenty four million, seven hundred and fifty five thousand, two hundred and twelve in symbols.
🔗
Solution.
In words In symbols
One hundred million \(100\,000\,000\)
Twenty four million \(24\,000\,000\)
Seven hundred thousand \(700\,000\)
Fifty five thousand \(55\,000\)
Two hundred \(200\)
Twelve \(12\)
\(124\,755\,212\)
Hence the given number in symbols is written as \(124\,755\,212\text{.}\)
🔗
🔗
🔗
🔗

Subsection 1.1.4 Reading and writing numbers in words.

Activity 1.1.4.

A customer wanted to deposit the cheque below and did not know the cheque worth.
🔗
1. Help the customer to read and write the value of the cheque in words.
🔗
2. Prepare dummy cheques similar to the one above.
🔗
3. Fill in the dummy cheques you have created with amounts of your choice and it should be a 6-digit number.
🔗
4. Read the amounts to your fellow learners.
🔗
🔗

Example 1.1.9.

The number of people who attended a cancer screening campaign in 2023 was 8 759 125. Read and write this number in words.
🔗
Solution.
Separate the digits in groups of threes starting from the ones place value. Write the total of each group.
🔗
\(8\,759\,125\) = \(8\,000\,000+ 759\,000 +125\)
🔗
\(8\,759\,125\) is Eight million, seven hundred and fifty nine thousand, one hundred and twenty five.
🔗
🔗
🔗

Example 1.1.10.

The price of a certain car in Kenya is \(3\,515\,252\) shillings. Write the price of the car in words.
🔗
Solution.
Use the concept of place value and total value as illustrated below to write the amount in words.
🔗
Digit Place value Total value Total value in words
3 Millions \(3\,000\,000\) Three million
5 Hundreds of thousands \(500\,000\) Five hundred thousand
1 Tens of thousands \(10\,000\) Ten thousand
5 Thousands 5 000 Five thousand
2 Hundreds \(200\) Two hundred
5 Tens \(50\) Fifty
2 Ones 2 Two
The price of the car in words is three million, five hundred and fifteen thousand, two hundred and fifty two.
🔗
🔗
🔗

Checkpoint 1.1.11.

find it on webwork
🔗
🔗
🔗

Subsection 1.1.5 Rounding off numbers to the nearest hundreds of million

To round off a number to the nearest hundreds of millions, we consider the digit in the tens of millions place value. If the digit is less than 5, we maintain the digit in the hundred of million place value and if the digit is \(5\) or greater, add one to the digit at the hundred thousand place value.
🔗

Activity 1.1.5.

1.(a) Study the place value chart below. It shows numbers \(469\, 852\, 231\) and \(623\,210\,140\) before and after rounding off.
🔗
Hundreds of millions Tens of millions Millions Hundreds of thousands Tens of thousands Thousands Hundreds Tens Ones
Original number 4 6 9 8 5 2 2 3 1
Rounded off number 5 0 0 0 0 0 0 0 0
Hundreds of millions Tens of millions Millions Hundreds of thousands Tens of thousands Thousands Hundreds Tens Ones
Original number 6 2 3 2 1 0 1 4 0
Rounded off number 6 0 0 0 0 0 0 0 0
(b) Compare the original number with the rounded off number. What do you notice?
🔗
(c) Discuss how to round off numbers to the nearest hundreds of million.
🔗
2. In turns, write different numbers and round them off to the nearest hundreds of million.
🔗
🔗

Example 1.1.12.

The number of malaria tablets that were produced by a pharmaceutical company over a certain period was 213 587 915. Round off this number to the nearest hundreds of million.
🔗
Solution.
To round off a number to the nearest hundreds of millions, we identify if the digit at the tens of millions place value is greater,less or equal to \(5\text{.}\)
🔗
If the digit in the tens of millions place value is greater or equal to \(5\) then add \(1\) to the digit in the hundreds of million place value and replace the remaining digits with zeros.
🔗
If the digit in the tens of millions place value is less than \(5\) then maintain the digit in the hundreds of million place value and replace the remaining digits with zeros.
🔗
Since the digit in the hundreds of millions place value is \(2\) and the digit in the tens of millions place value is \(1\text{,}\) we replace the digits on the right hand side of \(2\) with zeros.
🔗
Therefore, \(213\, 587 \,915\) to the nearest hundred million becomes \(200\, 000 \,000\)
🔗
🔗
🔗

Example 1.1.13.

Round off \(219\, 486\, 272\) to the nearest hundred million.
🔗
Solution.
Hundreds of millions Tens of millions Millions Hundreds of thousands Tens of thousands Thousands Hundreds Tens Ones
Original number 2 1 9 4 8 6 2 7 2
Rounded off number 2 0 0 0 0 0 0 0 0
The digit in the tens of million place value is \(1\text{.}\) Therefore, we retain digit \(2\) in the hundreds of millions place value and replace the remaining digits by zero.
🔗
\(219\, 486\, 272\) rounded off to the nearest hundred million is \(200\,000\,000\text{.}\)
🔗
🔗
🔗

Example 1.1.14.

Round off \(87\, 148\, 729\) to the nearest hundred million.
🔗
Solution.
Tens of millions Millions Hundreds of thousands Tens of thousands Thousands Hundreds Tens Ones
Original number 8 7 1 4 8 7 2 9
Rounded off number 9 0 0 0 0 0 0 0
To round off a number to the nearest tens of millions, we identify if the digit at the millions place value is greater,less or equal to \(5\text{.}\)
🔗
If the digit in the millions place value is greater or equal to \(5\) then add \(1\) to the digit in the tens of million place value and replace the remaining digits with zeros.
🔗
If the digit in the millions place value is less than \(5\) then maintain the digit in the tens of million place value and replace the remaining digits with zeros.
🔗
Digit \(7\) is in the place value of millions. We add one to digit \(8\) in the tens of millions place value and replace the remaining digits by zero.
🔗
\(87\, 148\, 729\) rounded off to the nearest ten million is \(90\,000\,000\text{.}\)
🔗
🔗
🔗

Checkpoint 1.1.15.

🔗

Checkpoint 1.1.16.

🔗
🔗

Subsection 1.1.6 Natural numbers

Subsubsection 1.1.6.1 Even numbers

Even numbers are numbers that are divisible by \(2\text{.}\)The digits in the ones place value are \(0,2,4,6 \) or \(8 \text{.}\)
🔗
Activity 1.1.6.
1.Think of a number between \(10\) and \(100\) and write down any \(5\) numbers.
🔗
2.Which of the numbers you wrote down are divisible by two?
🔗
3.Which digit is in the ones place value of each number that is divisible by two?
🔗
4.What do we call the numbers that are divisible by \(2\text{?}\)
🔗
5.Share your work with other learners.
🔗
🔗
Example 1.1.17.
Which of the following are even numbers?
🔗
\(127,3\,860,4\,249,58\,242,714\,931,96,3\,295\,418,5\,174\)
🔗
Solution.
\(3\,860,58\,242,96,3\,295\,418 \) and \(5\,174\) are even numbers since they are divisible by \(2\text{.}\) Also their digits in the ones place value are \(0,2,4,6\) \(\text{or}\) \(8\text{.}\)
🔗
🔗
🔗
Checkpoint 1.1.18.
check it on web work
🔗
🔗
🔗

Subsubsection 1.1.6.2 Odd numbers

Odd numbers are numbers that cannot be divided by two without leaving a remainder. The digit in the ones place value of an odd number is \(1,3,5,7\) or \(9\text{.}\)
🔗
Activity 1.1.7.
1. Outside the classroom, learners to stand in a circle and be assigned a number starting from \(1 \) to the last person.
🔗
2. The student assigned number \(1\) to stay standing and the student with number \(2\) will sit down first.
🔗
3. After number \(2\) sits, skip the next student at number \(3\) and ask the student with number \(4 \) to sit down. Fellow learners to shout out the next number to sit down.
🔗
4. Continue with this pattern where each student who sits down will skip the next student and have the student after them sit down. So after number \(4\) sits, number \(6\) will sit, then number \(8\text{,}\) and so on.
🔗
5. Once all even-numbered students have sat down, the students still standing will shout out their numbers one by one.
🔗
6. What are the last digits of the numbers the standing students shouted out?
🔗
7. What do we call numbers that are not divisible by \(2\text{?}\)
🔗
🔗
Example 1.1.19.
Which of the following are odd numbers?
🔗
\(22,57,124,769,1\,250,6\,545,17\,846,46\,541\)
🔗
Solution.
\(57,769,6\,545,46\,541\) are odd numbers since their digits in the ones place value are not divisible by two.
🔗
🔗
🔗
Checkpoint 1.1.20.
done on webwork
🔗
🔗
🔗
🔗

Subsection 1.1.7 Prime numbers

A prime number is a number that has only two divisors, that is, \(1\) and the number itself.
🔗
\(2\) is the only prime number that is even
🔗
\(1\) is not a prime number because it has only one divisor.
🔗

Activity 1.1.8.

1.Copy the table alongside.
🔗
Number Divisors
2 1,2
3
5
7
11
2.Work out the divisors of each number. Fill in the divisors column.
🔗
3.What is common in the numbers?
🔗
4.Share your findings with other learners in class and respect each others opinion
🔗
🔗

Example 1.1.21.

Which of the following numbers are prime numbers?
🔗
\(81,83,85,87,89\)
🔗
Solution.
List the divisors of all the numbers.
🔗
Choose the numbers that have \(2\) divisors only (one and the number itself)
🔗
Number Divisors
81 1,3,9,27,81
83 1,83
85 1,5,17,85
87 1,3,29,87
89 1,89
\(83\) and \(89\) are prime numbers since they have only two divisors.
🔗
🔗
🔗

Example 1.1.22.

Determine which of the following numbers are prime numbers.
🔗
Solution.
Use factor tree to identify the divisors of each number: \(2,3,4\text{.}\)
🔗
factors of 2
factors of 3
factors of 4
The divisors of \(2\) are \(2,1\text{.}\)
🔗
Divisors of \(3\) are \(3,1\) .
🔗
And the divisors of 4 are \(4,2,1\text{.}\)
🔗
Therefore, the numbers \(2\) and \(3\) are prime numbers.
🔗
🔗
🔗

Checkpoint 1.1.23.

🔗
🔗

Subsection 1.1.8 Operations on whole numbers

Subsubsection 1.1.8.1 Addition

Addition is a mathematical operation that involves combining two or more numbers to find their total. We use place value of digits to add numbers that is, while adding you allign the digits according to their place values.
🔗
Activity 1.1.9.
1. In groups of \(5\text{,}\) think of an addition word question and write it down on a blank paper. For example: Sera had \(56 \) guests at her birthday party in the morning and \(42\) more guests in the afternoon. How many guests attended her birthday party in total?
🔗
2. Work out the problem as a group and discuss how to add \(3,4, \text{or} 5\) - digit numbers i.e \(2543 + 678\)
🔗
3. Exchange the written word questions with other groups and work out each other’s question.
🔗
🔗
Example 1.1.24.
A company sold goods worth sh \(1\,478\,956,\) in the month of January. In February, the company sold goods worth sh \(2\,123\,040\text{.}\) What was the total sales in the two months?
🔗
Solution.
Add the amounts to get the total sales in two months.
🔗
+1 +1 +1 +1 +1 +1
1 4 7 8 9 5 6
2 5 6 2 3 9 8
+ 2 1 2 3 0 4 0
6 1 6 4 3 9 4
The total sales was sh \(6\,164\,394\)
🔗
🔗
🔗
Checkpoint 1.1.25.
🔗
🔗

Subsubsection 1.1.8.2 Subtraction of whole numbers

Activity 1.1.10.
Kahawa Tea company harvested \(326\,548\,957\) kilograms of tea. The company exported \(128\,349\,263\) kilograms of coffee.
🔗
1. Work out the kilograms of tea that remained after the export.
🔗
Share your work with fellow learners.
🔗
🔗
Example 1.1.26.
Fishermen across the country exported \(4\,563\,275\) kg of fish in the first year. In the second year; the mass of fish decreased by \(732\,738\) kg. Work out the mass of fish that the fishermen exported in the second year:
🔗
Solution.
First, subtract the decrease in mass of fish in the second year from the mass of fish in the first year.
🔗
3 10 2 10 6 10
\(\cancel{4}\) 5 6 \(\cancel{3}\) 2 \(\cancel{7}\) 5
- 7 3 2 7 3 8
3 8 3 0 5 3 7
If the digits in a column, starting from the right-hand side, result in a negative value when subtracted, you borrow from the first digit in the next column to the left..
🔗
The digit you borrow from will be reduced by 1, while the digit you borrow to will increase by 10. See the example above.
🔗
Therefore, the mass of fish the fisherman exported in the second year was \(3\,830\,537\) kg.
🔗
🔗
🔗
🔗

Subsubsection 1.1.8.3 Multiplication of whole number

Activity 1.1.11.
1. Make tables like the ones shown below.
🔗
3 4 5 6 7
8 27 35 40 54
78 63 82 91 44
132 217 810 514 231
72 60 42 56 79
852 147 320 560 801
332 133 249 900 448
5132 1217 3810 4514 6231
2.(a) In turns, choose one number from each table.
🔗
(b) Multiply the two numbers.
🔗
🔗
Example 1.1.27.
In the first phase of supplying books to schools, the government supplied \(723\) textbooks to each school. The number of schools that received the books was \(256\text{.}\) How many books did the government supply in the first phase?
🔗
Solution.
We multiply the number of books by the number of schools.
🔗
\(723\)
\(\times \, 256\)
\(4\,338\) (multiply 723 by the total value of the ones digit: 723 x 6)
\(36\,150\) (multiply 723 by the total value of the tens digit: 723 x 50)
\(+\, 144\,600\) (multiply 723 by the total value of the hundreds digit: 723 x 200)
\(185\,088\)
The number of books the government supplied is \(185\,088\text{.}\)
🔗
🔗
🔗
🔗

Subsubsection 1.1.8.4 Division of whole numbers

Sarah has 24 apples and wants to share them equally among \(6\) friends. To find out how many apples each friend gets, she divides \(24 ÷ 6 = 4\text{.}\) This means each friend receives \(4\) apples. Therefore, Sarah applies division to share the apples equally.
🔗
Activity 1.1.12.
1. Gather 30 books at the front of the classroom and form \(5\) groups.
🔗
2. In groups, discuss the number of books each group will get.
🔗
3. In turns, one student from each group to collect and place the book in their group tables untill there are no books left.
🔗
4. Each group to count the number of books they have. Did each group receive the same number of books? Was there a remainder?
🔗
5. Gather all books again and add \(7\) more then count them if it amounts to \(37\text{.}\)
🔗
6. In the same groups, follow the steps you used to divide \(30\) books to identify how many books each group will get.
🔗
7. Discuss if all books were equally distributed.
🔗
🔗
Example 1.1.28.
Work out the following:
🔗
a) \(6396 \div 123\)
🔗
b) \(2841 \div 45\)
🔗
Solution.
a).
🔗
\(52\)
\(123\) \(6396\)
- \(615\downarrow \)
\(246\)
\(-246\)
\(0\)
Therefore, \(6396 \div 123 = 52\)
🔗
b)
🔗
\(63\)
\(45\) \(2841\)
- \(270\downarrow \)
\(141\)
\(-135\)
\(6\)
\(2841 \div 45 = 63\) remainder \(6\text{.}\)
🔗
🔗
🔗
🔗

Subsubsection 1.1.8.5 Combined operations of whole numbers

Given a task that has combined operations, follow the following order to perform:
🔗
Division \(\rightarrow\) multiplication \(\rightarrow\) addition \(\rightarrow\) subtraction.
🔗
Figure 1.1.29. combined operations of whole numbers.
🔗
Activity 1.1.13.
Jerotich has \(3\) farms. She stored 90,000 litres of water using three tanks of equal size to irrigate the farms. One morning, she drew water from one tank to water the farms. Each farm used \(9200\) litres of water. Later in the evening, she added \(12 356\) litres of water into the tank she had drawn water from. She wondered what amount of water remained by the end of the day and she wanted to know the amount of water she needed to add to the tank in order to fill the tank to its original capacity.
🔗
In groups of \(5\text{,}\) help Jerotich identify the amount of water that remained in the tank by the end of the day and the capacity she needed to fill the tank to its original capacity.
🔗
🔗
Example 1.1.30.
Work out:
🔗
\(524 + 256 - 548 \div 4\)
🔗
Solution.
To solve for this, start with division i.e
🔗
\(548 \div 4\)
🔗
\(137\)
\(4\) \(548\)
\(-\) \(4\downarrow\downarrow \)
\(14\downarrow\)
\(-\) \(12\downarrow\)
\(28\)
\(-\) \(28\)
\(0\)
By performing division, the expression is reduced to :
🔗
\(524 + 256 - 137\)
🔗
Next we add: \(524 + 256 = 780\)
🔗
\(= 780 - 137 = 643\)
🔗
Therefore, \(524 + 256 - 548 \div 4 = 643\)
🔗
🔗
🔗
Example 1.1.31.
Work out:
🔗
\(546 \div 2 \times 12 - 1254 + 3546\)
🔗
Solution.
The task involves \(4\) operations and we perform it in the following order: division, multiplication, addition then subtraction.
🔗
\(546 \div 2 = 273\)
🔗
\(= 273 \times 12 - 1254 + 3546 \)
🔗
\(= 273 \times 12 = 3276\)
🔗
\(3276 - 1254 + 3546 \) rewriting this to perform addition we get:
🔗
\(3276 + 3546 = 6822\)
🔗
Finally, we subtract:
🔗
\(6822- 1254 = 5568\)
🔗
Therefore, \(546 \div 2 \times 12 - 1254 + 3546 = 5568\)
🔗
🔗
🔗
Figure 1.1.32. combined operations of whole numbers.
🔗
Checkpoint 1.1.33.
🔗
🔗
🔗

Subsection 1.1.9 Number sequence

A number sequence is a list of numbers that follow a specific pattern or rule.
🔗
Think of it like a list of numbers where each number is related to the one before it in a certain way e.g \(2, 4, 6, 8, 10, ...\) Here, you are adding 2 each time. These are all numbers that can be divided by 2.
🔗
The pattern could involve adding, subtracting, multiplying, or dividing by a certain number each time.
🔗

Subsubsection 1.1.9.1 Identifying a number sequence

\(\textbf{How to recognize a number sequence}\)
🔗
Look for the pattern. Identify if the numbers are increasing or decreasing. Find out if there is consistent amount being added or subtracted.
🔗
See if you can predict the next number based on the rule you find.
🔗
Activity 1.1.14.
1. Working in groups of \(5\text{,}\) each group to write down the following sequence:
🔗
  • Sequence: \(3\, ,6\,, 9\, ,12\,\text{,}\)___
    🔗
    🔗
  • Sequence: \(4\, ,8\, ,16\, ,32\, \text{,}\)___
    🔗
    🔗
  • Sequence: \(1\, ,4\, , 9\, ,16\,\text{,}\) ____
    🔗
    🔗
  • Sequence: \(1\, ,1\, ,2\,, 3\, ,5\, ,8\,\text{,}\) ___
    🔗
    🔗
🔗
2. Each team to take \(3\) minutes to solve each question and work together to identify the pattern and fill in the missing number.
🔗
3. At the end of 3 minutes, each group will present their answer to the class.
🔗
4. The group should explain the pattern they identified that is why it works and how they figured it out.
🔗
5. Discuss where you see number patterns in nature, technology, and everyday life.
🔗
🔗
Example 1.1.34.
Identify the missing number in the following sequences.
🔗
\(50\, ,400\,, 850\, ,1400\,\text{,}\)___,___,___
🔗
Solution.
1. The first step is to find the differences between consecutive numbers:
🔗
  • \(\displaystyle 400 - 50 = 350 \)
    🔗
    🔗
  • \(\displaystyle 850 - 400 = 450\)
    🔗
    🔗
  • \(\displaystyle 1400 - 850 = 550\)
    🔗
    🔗
🔗
So, the differences are \(350\, ,450\,, 550\,\) which are increasing by \(100\) each time.
🔗
2. Next step is to predict the next differences:
🔗
  • \(550 + 100 = 650\) (the next difference)
    🔗
    🔗
  • \(650 + 100 = 750\) (the following difference)
    🔗
    🔗
  • \(750 + 100 = 850 \)(the last difference)
    🔗
    🔗
🔗
3.Add these differences to the last known number (1400):
🔗
  • \(\displaystyle 1400 + 650 = 2050 \)
    🔗
    🔗
  • \(\displaystyle 2050 + 750 = 2800\)
    🔗
    🔗
  • \(\displaystyle 2800 + 850 = 3650\)
    🔗
    🔗
🔗
So the missing numbers are \(2050 \,,2800\,,3650 \)
🔗
4. Finally, the sequence is \(50\, ,400\,, 850\, ,1400\, ,2050\, ,2800\, ,3650\)
🔗
🔗
🔗
Example 1.1.35.
Rearrange the following numbers in ascending order and identify the next two numbers in each sequence.
🔗
\(648\, ,24\, ,216\,,8\,,72\)
🔗
Solution.
The given numbers are: \(648\,, 24\, ,216\, ,8\, ,72\) .
🔗
When rearranged in ascending order, we get:
🔗
\(8\, ,24\,, 72\, ,216\,, 648\text{.}\)
🔗
Now, let’s examine the relationship between the numbers:
🔗
  • \(\displaystyle 8 \times 3 = 24\)
    🔗
    🔗
  • \(\displaystyle 24 \times 3 = 72\)
    🔗
    🔗
  • \(\displaystyle 72 \times 3 = 216\)
    🔗
    🔗
  • \(\displaystyle 216 \times 3 = 648\)
    🔗
    🔗
🔗
From the above,each number is being multiplied by 3 to get the next number.
🔗
Therefore, the next \(2\) numbers are:
🔗
  • \(\displaystyle 648 \times 3 = 1944\)
    🔗
    🔗
  • \(\displaystyle 1944 \times 3 = 5832\)
    🔗
    🔗
🔗
The missing numbers are \(1944,5832\)
🔗
🔗
🔗
🔗

Subsubsection 1.1.9.2 Creating a number sequence

To create a number sequence, you need the first number in the sequence and the rule connecting the next numbers.
🔗
Activity 1.1.15.
There are 6 students in the class, and each student adds 2 books to a table. The 1st student places \(2\) books, the 2nd student places another \(2\text{,}\) and so on.
🔗
1. Record the total number of books as each student adds books on the table after each turn.
🔗
2. Figure out the sequence of books on the table and explore how patterns form.
🔗
3.Create different sequences using the same setup by changing the rules for adding books and generate new sequences i.e
🔗
  • Add an increasing number of books each time - this is a sequence where the 2nd student add 2, then third student 3, then forth student 4, and so on.
    🔗
    🔗
  • Each student can multiply the number of books added by the previous student like if previous student places \(2\) books the nextm will place \(4\) then the next will place\(8\text{.}\)
    🔗
    🔗
🔗
Each group to share their sequences with the class and explain the rule or pattern they used to generate their sequence .
🔗
🔗
Example 1.1.36.
Create a number sequence that starts at 60,000 upto the fifth term and follows the rule of dividing by 5.
🔗
Solution.
Since we have the 1st term and a rule, we can calculate the subsequent terms.
🔗
  • First term: \(60\,000 \)
    🔗
    🔗
  • Second term: \(60,000 ÷ 5 = 12\,000\)
    🔗
    🔗
  • Third term: \(12,000 ÷ 5 = 2\,400\)
    🔗
    🔗
  • Fourth term: \(2,400 ÷ 5 = 480\)
    🔗
    🔗
  • Fifth term: \(480 ÷ 5 = 96\)
    🔗
    🔗
🔗
The final sequence is: \(60\,000\, ,12\,000\, ,2\,400\, ,480\, ,96\)
🔗
🔗
🔗
Example 1.1.37.
Morara is a businessman. Every day, he deposits sh \(1,250\) into his bank account. Create a pattern to show his bank account balance at the end of each day for one week.
🔗
Solution.
Assume Morara starts with 0 shillings in his account at the beginning.
🔗
A week has \(7\) days and his account balance on the first day is sh \(1,250\text{.}\)
🔗
🔗
Therefore, the sequence of Morara’s bank account balance at the end of each day for one week is:
🔗
\(1250\, ,2500\, ,3750\, ,5000\,, 6250\, ,7500\, ,8750\)
🔗
🔗
🔗
🔗
🔗
🔗
PrevTopNext