Chapter 4 Analytic Geometry
The main topics of study in analytic geometry are straight lines and conic sections. Accordingly, by the end of this chapter you must
-
be able to derive basic equations that are representing straight lines, circles, parabolas, ellipses, and hyperbola.
-
know the main (important) properties of each of these five geometric objects.
-
be able to identify equations of straight lines, circles, parabolas, ellipses, hyperbolas and sketch their graphs.
More specific objectives are given in each section.
The major part of this chapter is \(\textbf{conic sections}\text{.}\) Conic sections are \(\textbf{circles}\text{,}\) \(\textbf{parabolas, ellipses}\) and \(\textbf{hyperbolas}\text{.}\) They are called conic sections because they are generated when a plane cuts a right circular double cone. Depending on how the plane cuts the cone the intersection forms a curve called a circle, an ellipse, a parabola or a hyperbola (See,(Figure 4.0.1)).
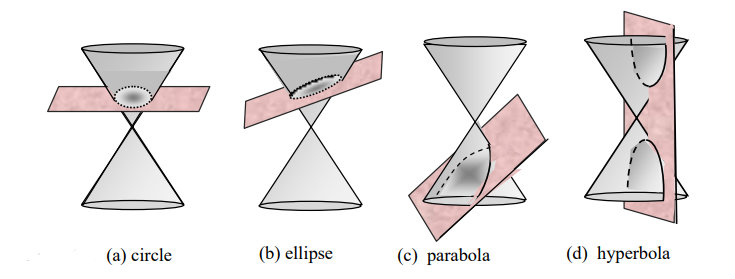
We will see that a conic section is described by a second degree equation in x and y of the form
\begin{equation*}
Ax^2 +Cy^2 + Ey +F =0
\end{equation*}
when A, C, D, E and F are constant real numbers. In the analysis of such equations we will frequently need the method of completing the square. Recall that completing the square is the method of converting an equation of the form
\begin{equation*}
x^2 + ax = b \quad \text{to} \quad (x+h)^2 = 0 \qquad
\end{equation*}
\begin{equation*}
\textbf{(can you establish the relationships between a,b and h,c?)}
\end{equation*}
To do this :- Add \(\left (\frac{a}{2} \right )^{2}\) to both sides of the former equation.
\begin{equation*}
\textbf{-Then complete the square of the resulting expression to get the later form.}
\end{equation*}
Here recall that:
\begin{equation*}
x^{2}+2ax+a^{2}=\left ( x+a \right )^{2} \quad \, \text{and} \quad \, x^{2}-2ax+a^{2}=\left ( x-a \right )^{2}
\end{equation*}
