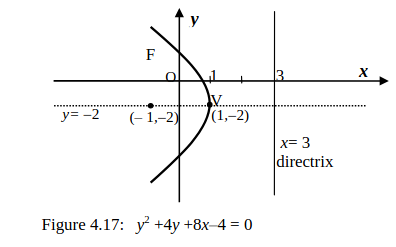Parabolas

Section 4.3 Parabolas

🔗

Objectives: Objectives

By the end of this section, you should:

🔗

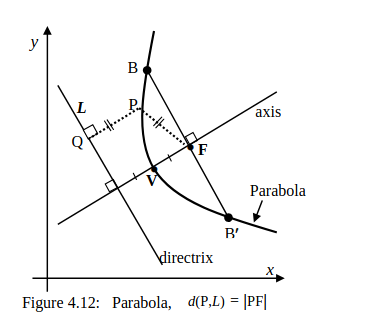
Know the geometric definition of a parabola.
🔗

🔗
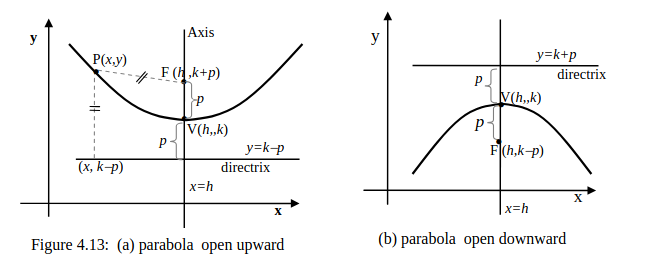
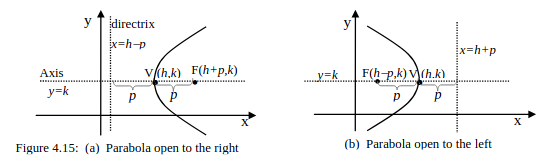
Know the meaning of vertex, focus, directrix, and axis of a parabola.
🔗

🔗
Be able to find equation of a parabola whose axis is horizontal or vertical.
🔗

🔗
Be able to identify equations representing sec-parabolas.
🔗

🔗
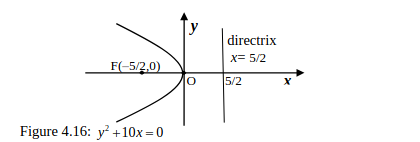
Be able to find the vertex, focus, and directrix of a parabola and sketch the parabola.
🔗

🔗

🔗

Subsection 4.3.1 Definition of a Parabola

Definition 4.3.1.

Let L be a fixed line and F be a fixed point not on the line, both lying on the plane. A parabola is a set of points equidistant from L and F. The line L is called the directrix and the fixed point F is called the focus of the parabola.

🔗

This definition is illustrated by Figure 4.12.

Note that the point halfway between the focus F and directrix \(L\) is on the parabola; it is called the \(\textbf{vertex},\) denoted by \(\text{V}\text{.}\)
🔗

🔗
VF| is called the \(\textbf{focal length}\text{.}\)
🔗

🔗
The line through F perpendicular to the directrix is called the \(\textbf{axis}\) of the parabola. It is the line of symmetry for the parabola.
🔗

🔗
The chord \(BB′ \)through \(\text{F} \) perpendicular to the axis is called \(\textbf{latus rectum}\text{.}\)
🔗

🔗
The length of the latus rectum, i.e, \(|BB′|\text{,}\) is called \(\textbf{focal width}\text{.}\)
🔗

🔗

🔗

Letting \(\textbf{|}VF \textbf{|} = \textbf{p}\text{,}\) you may show that \(\textbf{|}BB′\textbf{|} = 4p\text{;}\) i.e., focal width is \(4\) times focal length.

🔗

If \(\textbf{P}(x,y) \)is any point on the parabola, then by the definition, the distance of \(\textbf{P}\) from the directrix is equal to the distance between \(\text{P}\) and the focus \(\text{F}\text{.}\) This is used to determine an equation of a parabola. To do this, we consider first the cases when the axis of the parabola is parallel to one of the coordinate axes.

🔗

Exercises Exercises

1.

Use the definition of parabola and the given information to answer or solve each of the following problems.

🔗

Suppose the focal length of a parabola is \(p\text{,}\) for some \(p\) > 0. Then, show that the focal width (length of the latus rectum) of the parabola is \(4p\text{.}\)
🔗

🔗
Suppose the vertex of a parabola is the origin and its focus is\(\text{F}(0,1)\text{.}\) Then,
🔗
1. (a) What is the focal length of the parabola.
  🔗
  
  🔗
2. (b) Find the equations of the axis and directrix of the parabola.
  🔗
  
  🔗
3. (c) Find the endpoints of the latus rectum of the parabola.
  🔗
  
  🔗
4. (d) Determine whether each of the following point is on the parabola or not.
  🔗
  
  \((\text{i}) (4, 4) \,\,\,\,\,\, (\text{ii}) (2, 2) \,\,\,\,\,\, (\text{iii}) (-4, 4) \,\,\,\,\,\, (\text{iv}) (4, -4) \,\,\,\,\,\, (\text{v}) (1, \frac{1}{4})\)
  🔗
  
  (Note: By the definition, a point is on the parabola iff its distances from the focus and from the directrix are equal. )
  🔗
  
  🔗
🔗
🔗
Suppose the vertex of a parabola is \(\text{V}(0, 1)\) and its directrix is the line \(x = −2\text{.}\) Then,
🔗
1. Find the equation of the axis of the parabola.
  🔗
  
  🔗
2. Find the focus of the parabola.
  🔗
  
  🔗
3. Find the length and endpoints of the latus rectum of the parabola.
  🔗
  
  🔗
4. Determine whether each of the following point is on the parabola or not.
  🔗
  
  \((\text{i}) (1, 0)\,\,\,\,\,\,\, (\text{ii}) (3, 0)\,\,\,\,\,\,\, (\text{iii}) (8, 9) \,\,\,\,\,\,\, (\text{iv}) (8, -7) \,\,\,\,\,\,\, (\text{v}) (8, 8)\)
  🔗
  
  🔗
🔗
🔗

🔗

Checkpoint 4.3.2.

Add review

docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FAnalytic-Geometry-%28NS%29%2FDefinition-of-a-parabola%2FDeriving-the-Focal-Width-of-a-Parabola-from-its-Focal-Length.xml&entry.2077830997=source%2Fanalytic-geometry%2Fsections%2Fsubsections%2Fsec-parabolas%2Fsubsec-definition-of-a-parabola.ptx

🔗

Checkpoint 4.3.3.

Add review

docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FAnalytic-Geometry-%28NS%29%2FDefinition-of-a-parabola%2FProperties-of-a-Parabola-with-Origin-Vertex-and-given-Focus.xml&entry.2077830997=source%2Fanalytic-geometry%2Fsections%2Fsubsections%2Fsec-parabolas%2Fsubsec-definition-of-a-parabola.ptx

🔗

Subsection 4.3.2 Equation of Parabolas

I: Equation of a parabola whose axis is parallel to the \(y\)-axis:

🔗

A parabola whose axis is parallel to \(y\)-axis is called \(\textbf{vertical parabola}\text{.}\) A vertical parabola is either open upward (as in Figure 4.13 (a) ) or open downward (as in Figure 4.13 (b)).

🔗

Let \(p\) be the distance from vertex \(\text{V}(h,k)\) to the focus \(\text{F}\) of the parabola, i.e.,\(|VF| = p\text{.}\) Then, by the definition,\(\text{F}\) is located \(p\) units above \(\text{V} \)if the parabola opens upward and it is located \(p\) units below \(\text{V}\) if the parabola opens downward as indicated on Figure 4.13(a) and (b), respectively. To determine the desired equation, we first consider the case when the parabola opens upward.

🔗

Therefore, considering a vertical parabola with vertex \(\text{v(h,k)}\) that opens upward (Figure 4.13a), its focus is at \(\text{F(h, k+p})\text{.}\) \(\Rightarrow\) The equation of its directrix is \(\text{y = k−p.}\)

🔗

Then, for any point \(\text{P(x,y)} \) on the parabola, \(|PF|\) is equal to the distance between P and the directrix if and only if

🔗

\(\sqrt{(x-h)^2\, +\, (y-k-p)^2 } = y \,-\,k\,+\,p\)

🔗

Upon simplification, this becomes

🔗

\((x -h)^2 = 4p(y - k)\)

🔗

called standard equation of a vertical parabola, vertex \((h, k)\text{,}\) focal length \(p,\) open upward.
🔗

🔗

🔗

In particular, if the vertex of a vertical parabola is at origin, i.e., \((h, k) =(0,0)\) and opens upward, then its equation is

🔗

\(x^2 = 4py\)

🔗

( In this case, its focus is at \(\text{F(0, p)}\text{,}\) and its directrix is\(y = -p \text{.}\))
🔗

🔗

If a vertical parabola with vertex \(\text{V}(h, k)\) opens downward, then its directrix is above the parabola and its focus lies below the vertex (see Figure 4.13(b). In this case, the focus is at \(\text{F}(h, k−p)\text{,}\) and its directrix is given by \(y=k+p\text{.}\) Moreover, following the same steps as above , the equation of this parabola becomes

🔗

\((x - h)^2 = -4p(y - k)\)

🔗

( Standard equation of a vertical parabola, open downward, vertex \((h, k)\) , and focal length \(p .\) )
🔗

🔗

🔗

In particular, if the vertex of a vertical parabola is at origin, i.e., \((h, k) =(0,0)\) and opens downward, then it’s equation is

🔗

\(x^2 = -4py\)

🔗

( In this case, its focus is at\(\text{ F}(0,−p\)), and its directrix is \(y = p\) )

🔗

Example 4.3.4.

Find the vertex, focal length, focus and directrix of the parabola \(y\,=\,x^2\text{.}\)

🔗

Solution.

The given equation, \(x^2\,=\,y\text{,}\) is the standard equation of the parabola with vertex at origin \((0,0)\) and \(4p =1\) ⇒ its focal length is \(p\) = \(\frac{1}{4}\text{.}\) Since the parabola opens upward, its focus is \(p\) units above its vertex ⇒ its focus is at \(\text{F}(0,\frac{1}{4})\text{;}\) and its directrix is horizontal line \(p\) units below its vertex \(\Rightarrow\) its directrix is \(y\) = \(\frac{-1}{4}\text{.}\) You may sketch this parabola.

🔗

Example 4.3.5.

If a parabola opens upward and the endpoints of its latus rectum are at \(A(−4, 1)\) and \(B(2, 1)\text{,}\) then find the equation of the parabola, its directrix and sketch it.

🔗

Solution.

Since the focus \(F\) of the parabola is at the midpoint of its latus rectum \(AB\text{,}\) we have

\begin{align*} F = \amp(\frac{-4+2}{2}, \frac{1+1}{2})= (-1,1) \end{align*}

, and focal width

\begin{align*} 4p = |AB| =2-(-4) \amp=6 \end{align*}

\(\Rightarrow\) focal length \(p= 3/2.\) Moreover, as the parabola opens upward its vertex is \(p\) units below its focus. That is,

\begin{align*} \text{V}(h,k) = (-1,\, 1\,\frac{-3}{2}) = \amp (-1,\frac{-1}{2}). \end{align*}

Therefore, the equation of the parabola is

\begin{align*} (x+1)^2 = \amp 6(y+\frac{1}{2}) \end{align*}

🔗

And its directrix is horizontal line \(p\) units below its vertex, which is \(y = \frac{−1}{2} −\frac{3}{2} = −2\text{.}\)

🔗

The parabola is sketch in the Figure 4.14 .

🔗

II: Equation of a parabola whose axis is parallel to the \(x\)-axis.

🔗

A parabola whose axis is parallel to \(\textbf{x}\)-axis is called \(\textbf{horizontal parabola}\text{.}\) Such parabola opens either to the right or to the left as shown in Figure 4.15 (a) and (b), respectively.

🔗

The equations of such sec-parabolas can be obtained by interchanging the role of \(x\) and \(y\) in the equations of the sec-parabolas discussed previously. These equations are stated below. In both cases, let the vertex of the parabola be at \(\text{V}(h,k)\text{.}\)

🔗

If a horizontal parabola \(\textbf{opens to the right} \)(as in Fig.4.15(a) ), then its focus is to the right of \(\text{V}\) at \(\text{F}(h+p, k)\text{,}\) its directrix is \(x =h−p\text{,}\) and its equation is
🔗

\((y - k)^2 = 4p(x - h)\)
🔗

🔗
If a parabola \(\textbf{opens to the left }\)(as in Figure 4.15 (b) ), then its focus is to the left of \(\text{V}\) at \(\text{F}(h−p,k)\text{,}\) its directrix is \(x=h+p\) , and its equation is:
🔗

\((y - k)^2 = -4p(x - h)\)
🔗

🔗
If the vertices of these sec-parabolas are at the origin \((0,0)\text{,}\) then you can obtain their corresponding equations by setting \(h=0\) and \(k=0\) in the above equations.
🔗

🔗

🔗

Example 4.3.6.

Find the focus and directrix of the parabola \(y^2 = +10x = 0\) and sketch its graph.

🔗

Solution.

The equation is \(y^2 = -10x \text{;}\) and comparing this with the above equation, it is an equation of a parabola whose vertex is at \((0,0),\) axis of symmetry is the x-axis, open to the left and \(4p=10\text{,}\) i.e., \(p= 5/2\text{.}\) Thus, the focus is \(\text{F}=(–5/2,0)\) and its directrix is \(x = 5/2.\) Its graph is sketched in Figure 4.16.

🔗

\(\)

🔗

Example 4.3.7.

Find the focus and directrix of the parabola \(y^2 +4y +8x-4=0\) and sketch it.

🔗

Solution.

The equation is \(y^2 +4y = –8x +4\text{.}\) (Now complete the square of y-terms)

🔗

⇒

\begin{align*} y^2+4y+2^2 = \amp -8x+4+ 4 \end{align*}

🔗

⇒ \((y+2)^2 = –8x +8\)

🔗

⇒ \((y + 2)^2 = –8(x –1)\)

🔗

This is equation of a parabola with vertex at \((h, k) =(1,–2),\) open to the left and focal length \(p\text{,}\) where \(4p=8 \Rightarrow p=2\text{.}\) Therefore, its focus is

🔗

\(\text{F}= (h–p, k) = (–1, –2)\text{,}\) and directrix\(x=h+p =3\text{.}\) The parabola is sketched in Figure 4.17.

🔗

Remark 4.3.8.

An equation given as: \(\text{A}x^2 + \text{D}x + \text{E}y + \text{F} = 0\)

🔗

\(\text{C}y^2 + \text{D}x + \text{E}y + \text{F} = 0\)

🔗

may represent a parabola whose axis is parallel to the \(\textbf{y}\)-axis or parallel to the \(\textbf{x}\)-axis, respectively. The vertex, focal length and focus for such sec-parabolas can be identified after converting the equations into one of the standard forms by completing the square.

🔗

Checkpoint 4.3.9.

For questions 1 to 8, find an equation of the parabola with the given properties and sketch its graph.

Focus\((0, 1)\) and directrix \(y = −1.\)
🔗

2. Focus\((−1, 2) \)and directrix \(y= -2.\)
🔗

3. Focus\((3/2, 0)\) and directrix \(x= −3/2.\)
🔗

4. Focus \((−1, −2)\) and directrix \(x = 0.\)
🔗

5. Vertex\((3, 2 )\) and Focus\((3, 3)\text{.}\)
🔗

6. Vertex\((5, −2 )\) and Focus\((−5, −2).\)
🔗

7. Vertex\((1, 0)\) and directrix \(x = −2.\)
🔗

8. Vertex \((0, 2)\) and directrix \(y = 4.\)
🔗

🔗

🔗

For questions 9 to 17 find the vertex, focus and directrix of the parabola and sketch it.

🔗

9. \(y=2x^2\)

🔗

12. \(x+y^2=0\)

🔗

15.\(y^2 +8x+6y+5=0\)

🔗

10. \(8x^2=-y\)

🔗

13.\(x-1=(y+2)^2 \)

🔗

16. \(y^2 – 2y – 4x + 9= 0\)

🔗

11. \(4x − y^2= 0\)

🔗

14. \((x+4)^2 = 8y -24\)

🔗

17. \(-4x^2 +4x -\frac{1}{2}y=1\)

🔗

18. Find an equation of the parabola that has a vertical axis, its vertex at \((1, 0)\) and passing through \((0,1).\)

🔗

19. The vertex and endpoints of the latus rectum of the parabola \(x^2 = 36y\) forms a triangle. Find the area of the triangle.

🔗

20. P\((4, 6)\) is a point on a parabola whose focus is at \((0, 2) \) and directrix is parallel to \(x\)-axis.

🔗

(a) Find an equation of the parabola, its vertex and directrix.

🔗

(b) Determine the distance from P to the directrix.

🔗

21. An iron wire bent in the shape of a parabola has latus rectum of length 60cm. What is its focal length?

🔗

22. A cross-section of a parabolic reflector is shown in the figure below. A bulb is located at the focus and the opening at the focus,\(\text{AB, is} 12 \text{cm}\text{.}\) What is the diameter of the opening, \(\text{CD}, 8 \text{cm}\) from the vertex?

🔗

Checkpoint 4.3.10.

Add review

docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FAnalytic-Geometry-%28NS%29%2FEquation-of-a-parabola%2FFinding-Focus-and-Directrix-of-a-Parabola%28Guided%29.xml&entry.2077830997=source%2Fanalytic-geometry%2Fsections%2Fsubsections%2Fsec-parabolas%2Fsubsec-equation-of-parabolas.ptx

🔗

Checkpoint 4.3.11.

Add review

⁴

docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FAnalytic-Geometry-%28NS%29%2FEquation-of-a-parabola%2FFinding-the-Parabola-with-Given-Focus-and-Directrix.xml&entry.2077830997=source%2Fanalytic-geometry%2Fsections%2Fsubsections%2Fsec-parabolas%2Fsubsec-equation-of-parabolas.ptx

🔗

Checkpoint 4.3.12.

Add review

⁵

docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FAnalytic-Geometry-%28NS%29%2FEquation-of-a-parabola%2FFinding-Focus-and-Directrix-of-a-Parabola-%28Direct%29.xml&entry.2077830997=source%2Fanalytic-geometry%2Fsections%2Fsubsections%2Fsec-parabolas%2Fsubsec-equation-of-parabolas.ptx

🔗

Prev Top Next