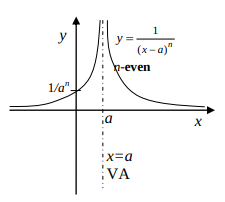
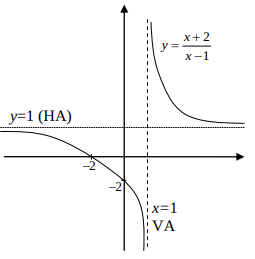
The functions described in this section frequently occur as mathematical models of real-life situations. For instance, in business the demand function gives the price per item,
\(p\text{,}\) in terms of the number of items sold,
\(x\text{.}\) Suppose a company finds that the price
\(p\) (in Birr) for its model GC-5 calculator is related to the number of calculators sold,
\(x\) (in millions), and is given by the demand function
\(p = 80 - x^{2}\text{.}\)
Zeros of a polynomial.
The zeros of a polynomial function provide valuable information that can be helpful in sketching its graph. One can find the zeros by factorizing the polynomial. However, we have no general method for factorizing polynomials of degree greater than
\(2\text{.}\) In this subsection, we turn our attention to methods that will allow us to find zeros of higher degree polynomials. To do this, we first need to discuss about the division algorithm. Recall that a number
\(a\) is a zero of a polynomial function
\(p\) if
\(p(a) = 0\text{.}\)
Division Algorithm.
Let
\(p(x)\) and
\(d(x)\) be polynomials with
\(d(x) \neq 0\text{,}\) and with the degree of
\(d(x)\) less than or equal to the degree of
\(p(x)\text{.}\) Then there are polynomials
\(q(x)\) and
\(R(x)\) such that
\(\underset{\text{dividend}}{\underbrace{p(x)}}
= \underset{\text{divisor}}{\underbrace{d(x)}} \cdot
\underset{\text{quotient}}{\underbrace{q(x)}} +
\underset{\text{remainder}}{\underbrace{R(x)}}
\text{,}\) where either
\(R(x) = 0\) or the degree of
\(R(x)\) is less than degree of
\(d(x)\)
Example 3.4.4.
Divide
\(\frac{x^{4} - 1}{x^{4} + 2x}\text{.}\)
Solution.
Using long division we have:
|
|
\(x^2 - 2x + 4\) |
|
|
| \(x^2 + 2x\) |
\(x^4 + 0x^3 + 0x^2 + 0x + 1\) |
|
\(- (x^4 + 2x^3)\) |
|
|
|
|
\(\quad \qquad -2x^3 + 0x^2\) |
|
|
|
\(\quad \quad- (-2x^3 - 4x^2)\) |
|
|
|
\(\qquad \qquad \qquad 4x^2 + 0x\) |
|
|
\(\qquad \qquad \qquad -(4x^2 + 8x)\) |
|
|
|
\(\qquad \quad -8x-1\) |
|
This long division means
\(\underset{\text{dividend}}{\underbrace{x^{4} - 1}}
= \underset{\text{divisor}}{\underbrace{(x^{2} + 2x)}} \cdot
\underset{\text{quotient}}{\underbrace{(x^{2} - 2x + 4)}} +
\underset{\text{remainder}}{\underbrace{(-8x - 1)}}\)
With the aid of the division algorithm, we can derive two important theorems that will allow us to recognize the zeros of polynomials.
If we apply the division algorithm where the divisor,
\(d(x)\text{,}\) is linear (that is of the form
\(x - r\)), we get
\begin{equation*}
\boxed{p(x)=(x-r)q(x)+R}
\end{equation*}
Note that since the divisor is of the first degree, the remainder
\(R\text{,}\) must be a constant. If we now substitute
\(x = r\text{,}\) into this equation, we get
\begin{equation*}
P(r)=(r-r)q(r)+R = 0 \cdot q(r)+R
\end{equation*}
Therefore,
\(p(r) = R\text{.}\)
The result we just proved is called the remainder theorem.
Theorem 3.4.5. The Remainder Theorem.
When a polynomial
\(p(x)\) of degree at least
\(1\) is divided by
\(x-r\text{,}\) then the remainder is
\(p(r)\text{.}\)
Example 3.4.6.
The remainder when
\(P(x) = x^{3} - x^{2} + 3x - 1\) is divided by
\(x - 2\) is
\(p(2) = 9\text{.}\) As a consequence of the remainder theorem, if
\(x - r\) is a factor of
\(p(x)\text{,}\) then the remainder must be
\(0\text{.}\) Conversely, if the remainder is 0, then
\(x - r\text{,}\) is a factor of
\(p(x)\text{.}\) This is known as the Factor Theorem.
Theorem 3.4.7. The Factor Theorem.
\(x - r\) is a factor of
\(p(x)\) if and only if
\(p(r) = 0\text{.}\)
The next theorem, called location theorem, allows us to verify that a zero exists somewhere within an interval of numbers, and can also be used to zoom in closer on a value.
Theorem 3.4.8. Location Theorem.
Let
\(f\) be a polynomial function and
\(a\) and
\(b\) be real numbers such that
\(a < b\text{.}\) If
\(f(a)f(b) < 0\text{,}\) then there is at least one zero of
\(f\) between
\(a\) and
\(b\text{.}\)
The Factor and Remainder theorems establish the intimate relationship between the factors of a polynomial
\(p(x)\) and its zeros. Recall that a polynomial of degree
\(n\) can have at most
\(n\) zeros. Does every polynomial have a zero? Our answer depends on the number system in which we are working. If we restrict ourselves to the set of real number system, then we are already familiar with the fact that the polynomial
\(p(x) = x^{2} + 1\) has no real zeros. However, this polynomial does have two zeros in the complex number system.(The zeros are
\(i\) and
\(- i\)). Carl Friedrich Gauss (
\(1777-1855\)), in his doctoral dissertation, proved that within the complex number system, every polynomial of degree
\(\geq 1\) has at least one zero. This fact is usually referred to as the Fundamental theorem of Algebra.
Theorem 3.4.9. Fundamental Theorem of Algebra.
If
\(p(x)\) is a polynomial of degree
\(n > 0\) whose coefficients are complex numbers, then
\(p(x)\) has at least one zero in the complex number system.
Note that since all real numbers are complex numbers, a polynomial with real coefficients also satisfies the Fundamental theorem of Algebra.As an immediate consequence of the Fundamental theorem of Algebra, we have
Theorem 3.4.10. The linear Factorization Theorem.
If
\(p(x) = a_{n}x^{n} + a_{n - 1}x^{n - 1} + \cdots + a_{1}x + a_{0}\text{,}\) where
\(n \geq 1\) and
\(a_{n} \neq 0\text{,}\) then
\(p(x)=a_{n}(x-r_{1})(x-r_{2})\ldots (x-r_{n})\text{,}\) where
\(r_{i}\) are complex numbers (possible real not necessarily distinct).
From the linear factorization theorem, it follows that every polynomial of degree
\(n \geq 1\) has exactly
\(n\) zeros in the complex number system, where a root of multiplicity
\(k\) counted
\(k\) times.
Example 3.4.11.
Express each of the polynomials in the form described by the Linear Factorization Theorem. List each zero and its multiplicity.
-
\(\displaystyle p(x)= x^{3}-6x^{2}-16x\)
-
\(\displaystyle q(x)=3x^{2}- 10x +8\)
-
\(\displaystyle f(x)= 2x{4}+8x^{3}+10x^{2}\)
Solution.
-
We may factorize
\(p(x)\) as follows:
\begin{align*}
p(x)= x^{3}-(6)x^{2}-16x=\amp x(x^{2} - 6x - 16) \\
=\amp x(x-8)(x+2) \\
=\amp x(x-8)(x-(x-2))
\end{align*}
The zeros of
\(p(x)\) are
\(0, 8,\) and
\(–2\) each of multiplicity one.
-
We may factorize
\(q(x)\) as follows:
\begin{align*}
q(x) = 3x^{2} - 10x + 8 \amp= (3x - 4)(x - 2)\\
\amp= 3(x - \frac{4}{3})(x - 2)
\end{align*}
Thus, the zeros of
\(q(x)\) are
\(\frac{4}{3}\) and
\(2\text{,}\) each of multiplicity one.
-
We may factorize
\(f(x)\) as follows:
\begin{align*}
f(x) = 2x^{4} + 8x^{3} + 10x^{2} =\amp 2x^{2}(x^{2} + 4x + 5)\\
=\amp 2x^{2}(x - (-2 + i))(x - (-2 - i))
\end{align*}
Thus, the zeros of
\(f(x)\) are
\(0\) with multiplicity two and
\(- 2 + i\) and
\(- 2 - i\) each with multiplicity one.
Example 3.4.12.
-
Find a polynomial
\(p(x)\) with exactly the following zeros and multiplicity.
| \(-1\) |
\(3\) |
| \(2\) |
\(4\) |
| \(5\) |
\(2\) |
Are there any other polynomials that give the same roots and multiplicity?
-
Find a polynomial
\(f (x)\) having the zeros described in part (a) such that
\(f(1) = 32\text{.}\)
Solution.
-
Based on the Factor Theorem, we may write the polynomial as
\(p(x)\ = (x - ( - 1))^{3}\ (x - 2)^{4}(x - 5)^{2} = (x + 1)^{3}\ (x - 2)^{4}(x - 5)^{2}\) which gives the required roots and multiplicities.
Any polynomial of the form
\(kp(x)\text{,}\) where
\(k\) is a non-zero constant will give the same roots and multiplicities.
-
Based on part (1), we know that \(f(x) = k(x + 1)^{3}\ (x - 2)^{4}(x - 5)^{2}\text{.}\) Since we want \(f(x) = 32\text{,}\) we have
\begin{align*}
f(1) \amp = k(1+1)^3 (1-2)^4 (1-5)^2 \\
32 \amp= k(8)(1)(16) \Rightarrow k = \frac{1}{4}
\end{align*}
Thus, \(f(x) = \frac{1}{4}(x + 1)^{3}\ (x - 2)^{4}(x - 5)^{2}\text{.}\)
Our experience in using the quadratic formula on quadratic equations with real coefficients has shown us that complex roots always appear in conjugate pairs. For example, the roots of
\(x^{2}-2x+5 = 0\) are
\(1+2 i\) and
\(1-2 i\text{.}\) Infact, this property extends to all polynomial equations.
Theorem 3.4.13. Conjugate Roots Theorem.
Let
\(p(x)\) be a polynomial with real coefficients. If complex number
\(a + bi\) (where
\(a\) and
\(b\) are real numbers) is a zero of
\(p(x)\text{,}\) then so is its conjugate
\(a - bi\text{.}\)
Example 3.4.14.
Let
\(r(x) = x^{4} + 2x^{3} - 9x^{2} + 26x - 20\text{.}\) Given that
\(1 - \sqrt{3} i\) is a zero, find the other zero of
\(r(x)\text{.}\)
Solution.
According to the Conjugate Roots Theorem, if
\(1 - \sqrt{3} i\) is a zero, then its conjugate,
\(1 + \sqrt{3} i\) must also be a zero. Therefore,
\(x - (1 - \sqrt{3} i)\) and
\(x - (1 + \sqrt{3} i )\) are both factors of
\(r(x)\text{,}\) and so their product must be a factor of
\(r(x)\text{.}\) That is,
\(\lbrack x - (1 - \sqrt{3} i )\rbrack\) \(\lbrack x - (1 + \sqrt{3} i )\rbrack =\) \(x^{2} - 2x + 4\) is a factor of
\(r(x)\text{.}\) Dividing
\(r(x)\) by
\(x^{2} - 2x + 4\text{,}\) we obtain
\begin{equation*}
r(x) = (x^2-2x+4)(x^2+4x-5) = (x^2 - 2x + 4)(x+5)(x-1).
\end{equation*}
Thus, the zeros of
\(r(x)\) are
\(1 - \sqrt{3} i\text{,}\) \(1 + \sqrt{3} i\text{,}\) \(- 5\) and
\(1\text{.}\)
The theorems we have discussed so far are called existence theorems because they ensure the existence of zeros and linear factors of polynomials. These theorems do not tell us how to find the zeros or the linear factors. The Linear Factorization Theorem guarantees that we can factor a polynomial of degree at least one into linear factors, but it does not tell us how.
We know from experience that if
\(p(x)\) happens to be a quadratic function, then we may find the zeros of
\(p(x) = Ax^{2} + Bx + C\) by using the quadratic formula to obtain the zeros
\begin{equation*}
x = \frac{- B \pm \sqrt{B^{2} - 4A}}{2A}\text{.}
\end{equation*}
The rest of this subsection is devoted to developing some special methods for finding the zeros of a polynomial function.
As we have seen, even though we have no general techniques for factorizing polynomials of degree greater than
\(2\text{,}\) if we happen to know a root, say
\(r\text{,}\) we can use long division to divide
\(p(x)\) by
\(x - r\) and obtain a quotient polynomial of lower degree. If we can get the quotient polynomial down to a quadratic, then we are able to determine all the roots. But how do we find a root to start the process? The following theorem can be most helpful.
Theorem 3.4.15. The Rational Root Theorem.
Suppose that
\(f(x) = a_{n}x^{n} + a_{n - 1}x^{n - 1} + \cdots + a_{1}x + a_{0}\text{,}\) where
\(n \geq 1\ ,\ a_{n} \neq 0\) is an
\(n^{\text{th}}\) degree polynomial with integer coefficients. If
\(\frac{p}{q}\) is a rational root of
\(f(x) = 0\text{,}\) where
\(p\) and
\(q\) have no common factor other than
\(\pm 1\text{,}\) then
\(p\) is a factor of
\(a_{0}\) and
\(q\) is a factor of
\(a_{n}\text{.}\)
To get a feeling as to why this theorem is true, suppose
\(\frac{3}{2}\) is a root of
\(a_{3}x^{3} + a_{2}x^{2} + a_{1}x + a_{0} = 0\text{.}\)
Then,
\(a_{3}\left( \frac{3}{2} \right)^{3} + a_{2}\left( \frac{3}{2} \right)^{2} + a_{1}
\left( \frac{3}{2} \right) + a_{0} = 0\) which implies that
\begin{equation*}
\frac{27a_{3}}{8} + \frac{9a_{2}}{4} + \frac{3a_{1}}{2} + a_{0} = 0 \text{ multiplying both sides by } 8
\end{equation*}
\begin{equation}
27a_{3} + 18a_{2} + 12a_{1} = - 8a_{0}\tag{3.4.1}
\end{equation}
\begin{equation}
27a_{3} = - 18a_{2} - 12a_{1} - 8a_{0}\tag{3.4.2}
\end{equation}
If we look at equation
(3.4.1), the left hand side is divisible by
\(3\text{,}\) and therefore the right hand side must also be divisible by
\(3\text{.}\) Since
\(8\) is not divisible by
\(3\text{,}\) \(a_{0}\) must be divisible by
\(3\text{.}\) From equation
(3.4.2),
\(a_{3}\) must be divisible by
\(2\text{.}\)
Example 3.4.16.
Find all the zeros of the function
\(p(x) = 2x^{3} + 3x^{2} - 23x - 12\)
Solution.
According to the Rational Root Theorem, if
\(\frac{p}{q}\) is a rational root of the given equation, then
\(p\) must be a factor of
\(-12\) and
\(q\) must be a factor of
\(2\text{.}\) Thus, we have
possible values of
\(p\text{:}\) \(\pm 1, \pm 2, \pm 3, \pm 4, \pm 6, \pm 12\)
possible values of
\(q\text{:}\) \(\pm 1, \pm 2\)
possible rational roots
\(\frac{p}{q}\text{:}\) \(\pm 1, \pm \ \frac{1}{2},\ \pm 2,
\pm 3,\ \pm \frac{3}{2}, \pm 4, \pm 6, \pm 12\)
We may check these possible roots by substituting the value in
\(p(x)\text{.}\) Now
\(p(1) = - 30\) and
\(p( - 1) = 12\text{.}\) Since
\(p(1)\) is negative and
\(p( - 1)\) is positive, by location theorem,
\(p(x)\) has a zero between
\(- 1\) and 1. Since
\(P\left( - \frac{1}{2} \right) = 0\text{,}\) then
\(\left( x + \frac{1}{2} \right)\) is a factor of
\(p(x)\text{.}\) Using long division, we obtain
\(\begin{matrix}
p(x) = 2x^{3} + 3x^{2} - 23x - 12 \amp = (x + \frac{1}{2})(2x^{2} + 2x - 24) \\
\amp = 2(x + \frac{1}{2})(x + 4)(x - 3) \\
\end{matrix}\)
Therefore, the zeros of
\(p(x)\) are
\(- \frac{1}{2}\text{,}\) \(- 4\) and
\(3\text{.}\)