Subsection 4.5.2 Equation of a hyperbola
We are now ready to derive equation of a hyperbola. But, for simplicity, we consider first the equation of a standard hyperbola with center at origin. A standard hyperbola is the one whose principal axis (or transverse axis) is parallel to either of the coordinate axes.
I. Equation of a standard hyperbola with center at origin.
There are two possible situations, namely, when the transverse axis lies on
x-axis (called horizontal hyperbola) and when the transverse axis lies on
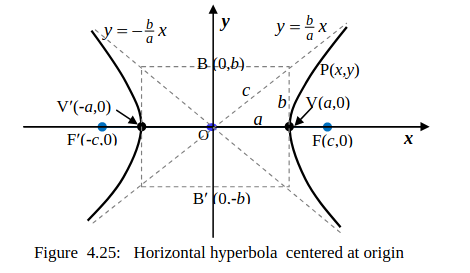
y-axis (called vertical hyperbola). We first consider a horizontal hyperbola with center C(0,0), vertices V′(−
a, 0), V (
a, 0) and foci
Notice that
\(c^2\) −
\(a^2\) > 0 as
c >
a . Hence, we can put
\(b^2 = C^2 - a^2\)for some positive
b. That is,
\(a^2 + b^2 = C^2 \) so that
a,
b, c are sides of a right triangle (see, Figure 4.25). The line segment BB′ perpendicular to the transverse axis at C and with endpoints B(0,
b) and B′(0,−
b) is called
conjugate axis of the hyperbola. Observe that the midpoint of the conjugate axis is C and its length is |BB′
| = 2
b. (
b will play important role in equation of the hyperbola and its graph).
Now, for any point P(
x,y) on the hyperbola it holds that
|PF′
| − |PF
| = 2
a .
That is,
\(\sqrt{(x+c)^2 + y^2} - \sqrt{(x-c)^2 + y^2 = 2a}\)
or
\(\sqrt{(x+c)^2 + y^2} = 2a + \sqrt{(x-c)^2 + y^2 }\)
Squaring both sides we get
\(x^2 + 2cx + c^2 + y^2 = 4a^2 + 4a \sqrt{(x-c)^2 + y^2} + x^2 - 2cx + c^2+ y^2\)
which simplifies to
\(a \sqrt{(x-c)^2) + y^2} = cx - a^2\)
Again squaring both sides and rearranging, we get
\((c^2 - a^2 )x^2- y^2 = a^2 (c^2-a^2+y^2)\)
Recall that we set
\(b^2 = C^2 - a^2\text{.}\) So, using this in the above equation and dividing both sides by
\(a^2b^2\), the equation becomes
\(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\)
(Equation of horizontal hyperbola with center C(0,0)
, vertices
\((\pm \text{a}, 0)\text{,}\) foci
\((\pm \text{c}, 0)\text{,}\) where
\(\pm \text{c}2\) =
\(\text{a}2\) +
\(b\text{2}\) )
Note that this hyperbola has no
y-intercept because if
x = 0, then −
\(y^2\) =
\(b^2\) which is not possible. The hyperbola is symmetric with respect to both
x-and
y- axes.
Also, from this equation we get
\(\frac{x^2}{a^2} = 1 + \frac{y^2}{b^2} \geq 1\) implies that
\(x^2 \geq a^2\) . So,
\(|x| = \sqrt{x^2} \geq \sqrt{a^2} = a \).
Therefore, we have
x ≥
a or
x ≤ −
a. This means that the hyperbola consists of two parts, called its
branches. Moreover, if we solve for
y from the equation we get
\(y = \pm \frac{b}{a} \sqrt{x^2 - a^2} \rightarrow \pm \frac{b}{a}\) as
x → ∞.
This means the hyperbola will approach (but never reaches) the line
\(y = \pm \frac{b}{a}x\) as
x gets larger and larger. That is, the lines
\(y = \pm \frac{b}{a}x\) are the
asymptotes of the hyperbola.
In sketching a hyperbola, it is best to draw the rectangle formed by the line
y = ±
b and
x = ±
a and the to draw the asymptotes which are along the diagonals of the rectangle (as shown by the dashed lines in Figure 4.25). The hyperbola lies outside the rectangle and inside the asymptotes. It opens around the foci.
Example 4.5.4.
Find the foci and equation of the hyperbola with vertices F′(−5, 0) and F(5, 0) and passing through P(5, 16/3).
Solution.
It is horizontal hyperbola with center (0,0) and
c = 5. In addition, as P(5, 16/3) is on the hyperbola we have that
|PF′
| − |PF
| = 2
a. That is,
\(\sqrt{(5 + 5)^2 +( \frac{16}{3})^2} - \sqrt{(5 - 5)^2 +( \frac{16}{3})^2} = 2a\)
⇒
a =3. (So, its vertices are (−3, 0) and (3, 0) ).
Now, using the relationship
\(b^2\) =
\(c^2\) -
\(a^2\), we have
\(b^2 = 25 -9 =16 \text{.}\)
Therefore, the equation of the hyperbola is
\(\frac{x^2}{9} - \frac{y^2}{16} = 1\)
You may find the asymptotes and sketch the hyperbola.
For a vertical hyperbola with center at origin (i.e., when transverse axis lies on
y-axis), by reversing the role of
x and
y we obtain the following equation which is illustrated in Figure 4.26.
\(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\)
( Equation of vertical hyperbola with center C(0,0)
,foci (0, ±
\(c^2\)), vertices (0, ±
a), where
c =
\(a^2\) +
\(b^2\)and asymptotes
\(y = ±(a/b)x )\)
Note:
-
For a vertical hyperbola, the coefficient of
\(y^2\)is positive and that of
\(x^2\)is negative.
-
\(a^2\)is always the denominator of the positive term.
Example 4.5.5.
Find the foci and equation of the hyperbola with vertices V′(0,−1) and V(0, 1) and an asymptote
\(y=2x.\)
Solution.
It is a vertical hyperbola with center C(0,0) and a = |CV| = 1. Since an asymptote of such vertical hyperbola is
\(y = {a/b}x\) and the slope of the given asymptote is 2, we have a/b = 2 ⇒ 1 /b =2 ⇒
b = 1/2. Thus,
\(c^2\) =
\(a^2\)+
\(b^2\)\(= 1 + 1/4 = 5/4 \text{.}\)
So, the foci are
\(0, \sqrt{5}/2\)and the equation of the hyperbola is
\(y^2\) − 4
\(x^2 = 1.\)
(You may sketch the hyperbola)
(II) Equation of shifted sec-hyperbolas:
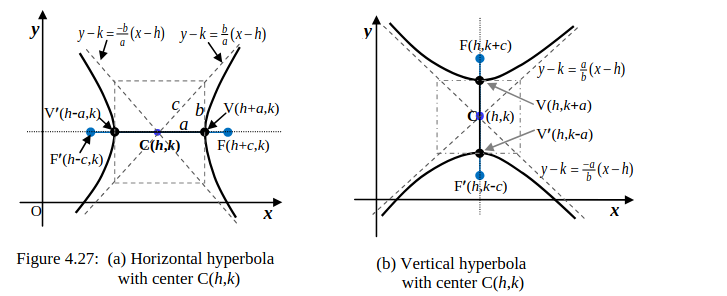
The center of a horizontal or vertical hyperbola may be not at origin but at some other point C(
h,k) as shown in Figure 4.27. In this case, we form the equation of the sec-hyperbolas by using the translation of the
xy-coordinate system that shifts its origin to the point C(
h,
k). As discussed in Section 4.4, the effect of this translation is just replacing
x and
y by
\(x−h\)and
\(y−k\text{,}\) respectively, in the equation of the desired hyperbola.
\(y-k = \frac{-a}{b}(x-h)\)
Therefore, the standard equation of a horizontal hyperbola (transverse axis parallel to
x-axis) with center C(
h,k), length of transverse axis =2
a, and length of conjugate axis =2
b is
\(\frac{(x - h)^2} {a^2} - \frac{(y - k)^2}{b^2} = 1\)
-
Vertices: V′ (
h–a,k), V(
h+a, k)
Foci : F′(
h–c, k), F(
h+
c,
k), where
\(c^2\)=
\(a^2\) +
\(b^2\)
Asymptotes:
\(y-k = \pm \frac{b}{a}(x-h)\)
Similarly, the standard equation of a vertical hyperbola (transverse axis parallel to
y-axis) with center C(
h,k), length of transverse axis =2
a, and length of conjugate axis =2
b is
\(\frac{(y - k)^2} {a^2} - \frac{(x - h)^2}{b^2} = 1\)
-
Vertices: V′ (
h,k–a), V(
h, k+a),
Foci : F′(
h, k–c), F(
h, k+
c), where
\(c^2\) =
\(a^2\) +
\(b^2\)
Asymptotes:
\(y - k = \pm \frac{a}{b}(x-h)\)
Example 4.5.6.
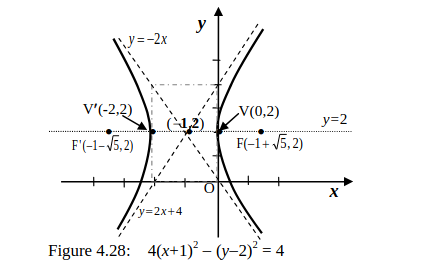
Find the foci, vertices and the asymptotes of the hyperbola whose equation is
\(4(x+1)^2 − (y−2)^2 = 4\) and sketch the hyperbola.
Solution.
Dividing both sides of the equation by 4 yields
\((x+1)^2 - \frac{(y-2)^2}{4}=1.\)
This is equation of a hyperbola with center
\(\text{C}(−1, 2)\text{.}\) Note that the ’
\(x^2\)term’ is positive indicates that the hyperbola is horizontal (principal axis
y=2),
a=1,
b=2, and
\(c^2\)=
\(a^2\)+
\(b^2\) ⇒
\(C = \sqrt{5}\text{.}\) As a result the foci are at
\((-1 \,- \sqrt{5},2)\) and
\((-1 \,+ \sqrt{5},2)\text{,}\) vertices are at
\((−2,2)\) and
\((0,2) \) and the asymptotes are the lines
\(y−2=\,±2(x+1)\text{,}\) that is,
\(y=2x+4 \) and
\(y=−2x\text{.}\) Consequently, the hyperbola is sketched as in Figure 4.28.
\begin{align*}
\text{F}(-1 +\sqrt{5},2) \amp
\end{align*}
Example 4.5.7.
Find the foci of the conic
\(9x^2 -4y^2 -72x+8y+176 =0\) and sketch its graph.
Solution.
Group the
x-terms and
y-terms of the equation and complete their squares:
\begin{align*}
\,\,\, \Rightarrow 9x^2 -4y^2 -72x+8y \amp = -176
\end{align*}
(Multiply both sides by -1)
\(\,\,\, \Rightarrow 9x^2 + 72x + 4y^2 -8y \amp = 176\) \(\,\,\, \Rightarrow -9x^2 + 72x + 4y^2 -8y \amp = -176\) \(\,\,\, \Rightarrow 4(y^2-2y) - 9(x^2 -8x) \amp = 176\) \(\,\,\, \Rightarrow 4(y^2-2y ) {\color{Blue} \textbf{+ }1^2} - 9(x^2 - 8x ) {\color{Blue}\textbf{+} 4^2 } \amp = 176 {\color{Blue} \textbf{+ 4 -144}} \)
\(\,\,\, \Rightarrow 4(y-1)^2 - 9(x - 4 )^2 \amp = 36 \)
(Next, divide each by 36)
\(\,\,\, \Rightarrow \frac{(y-1)^2}{ 9} - \frac{(x - 4 )^2 }{4}\amp = 1 \)
This is standard equation of a hyperbola whose transverse axis is parallel to the y-axis (as its ’
\(b^2\) term’ is positive) with center C
\((4,1)\text{,}\) \(a^2=9\) and
\(b^2 =4\) . ⇒
\(c^2 = b^2 + a^2 =13 ⇒ c = \sqrt{13} \text{.}\) Thus, foci are F′
\((4,1 - \sqrt{13})\) and F
\((4,1 + \sqrt{13})\text{,}\) and vertices
\((4,1 \pm3)\text{,}\) i.e,, V′
\((4,–2) \) and V
\((4,4)\text{.}\) Moreover, the asymptotes are y Hence, the asymptotes are
\(l_1\):
\(y-1 = \frac{3}{2}(x - 4) \) and
\(l_2:\) :
\(y -1 = -\frac{3}{2}(x - 4)\text{.}\) The hyperbola is sketched in Figure 4.29
Example 4.5.8.
Determine the locus or type of the conic section given by the equation
\(-x^2 + y^2 + 4x -2y = 3\)
Solution.
Grouping the
x-terms and
y-terms of the equation and completing their squares yield
\begin{align*}
(y-1)^2 - ( x-2)^2 = \amp 0\\
\,\,\, \Rightarrow (y-1)^2 = \amp (x -x2)^2\\
\,\,\, \Rightarrow y - 1 = \amp \pm \sqrt{(x-2)^2} = \pm (x-2)
\end{align*}
This represents pair of two lines intersecting at (2, 1), namely,
y =
x−1 and
y = −
x+3.
Exercises Exercises
1.
For questions 1 to 9, find an equation of the hyperbola having the given properties and sketch its graph.
1. Center at the origin, a focus at
\((5, 0)\text{,}\) and a vertex at
\((3, 0)\)
2. Center at the origin, a focus at
\((0,−5)\text{,}\) and a vertex at
\((0, −3)\text{.}\)
3. Center at the origin,
x-intercepts ±3, an asymptote
y = 2
x .
4. Center at the origin, a vertex at
\((2, 0)\) , and passing through
\((4, \sqrt{3})\text{.}\)
5. Center at
\((4, 2)\text{,}\) a vertex at
\((7, 2)\) , and an asymptote
\(3y = 4x−10.\)
6. Foci at
\((–2, –1)\) and
\(\text{F}_2\text{,}\) length of transverse axis 6.
7. Foci at
\((1, 3)\) and
\((7, 3)\text{,}\) and vertices at
\((2,3)\) and
\((6, 3)\text{.}\)
8. Vertices at (±3, 0), and asymptotes
\(y = ±\, 2x\)
9. Eccentricity
e\(=1\).\(5\text{,}\) endpoints of transversal axis at
\((2,2)\)and
\((6,2)\text{.}\)
For questions 10 to 17 find the center, foci, vertices and asymptotes of the hyperbola having the given equation and sketch its graph.
10.
\(\frac{x^2}{64} - \frac{y^2}{36} = 1\)
14.
\(\frac{(x - 2)^2}{9} - \frac{(y + 3)^2}{16} = 1\)
15.
\(4x^2 - y^2 + 2y - 5 = 0\)
16.
\(2x^2 - 3y^2 - 4x + 12y + 8 = 0\)
13.
\((y + 1)^2 - 4(y + 2)^2 = 8\)
17.
\(-16x^2 + 9y^2 - 64x + 90y + 305 = 0\)
18. Find an equation of hyperbola whose major axis is parallel to the x-axis, has a focus at
\((2,1)\)and its vertices are at the endpoints of a diameter of the circle
\(x^2 + y^2 -2y =0\)
19. A satellite moves along a hyperbolic curve whose horizontal transverse axis is 24 km and an asymptote
\(y = \frac{5}{12} \text{x} + 2\text{.}\) Then what is the eccentricity of the hyperbola?
20 Two regions A and B are separated by a sea. The shores are roughly in a shape of hyperbolic curves with asymptotes
\(y = \pm 3x\)and a focus at
\((30,0)\) taking a coordinate system with origin at the center of the hyperbola. What is the shortest distance between the regions in kms?
21. Determine the type of curve represented by the equation
\(\frac{x^2}{k} + \frac{y^2}{k-16} = 1\)
In each of the following cases: ( a)
\(k < 0,\) (b)
\(0 < k < 16,\) (c)
\(k >16 \)
Checkpoint 4.5.10.
Checkpoint 4.5.11.
Checkpoint 4.5.12.
Checkpoint 4.5.13.