Circles

Section 4.2 Circles

By the end of this section, you should

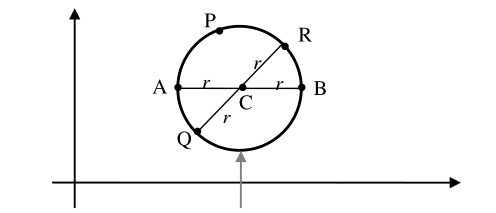
know the geometric definition of a circle.
🔗

🔗
be able to identify whether a given point is on, inside or outside a circle.
🔗

🔗
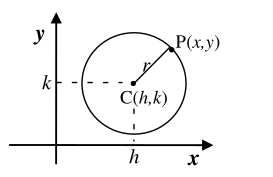
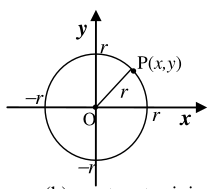
be able to construct equation of a circle.
🔗

🔗
be able to identify equations that represent circles
🔗

🔗
be able to find the center and radius of a circle and sketch its graph if its equation is given.
🔗

🔗
be able to identify whether a given circle and a line intersect at two points, one points or never intersect at all.
🔗

🔗
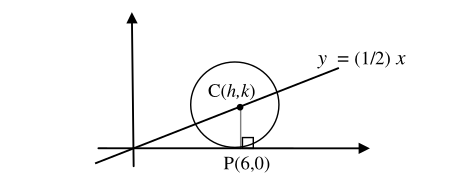
know the properties of a tangent line to a circle.
🔗

🔗
be able to find equation of a tangent line to a circle.
🔗

🔗

Subsection 4.2.1 Definition of a Circle

Definition 4.2.1.

A circle is the locus of points (set of points) in a plane each of which is equidistant from a fixed point in the plane. The fixed point is called the center of the circle and the constant distance is called its radius.

🔗

Definition 4.2.1 is illustrated by Figure 4.6 in which the center of the circle is denoted by ’’C’’ and its radius is denoted by r.

🔗

Figure 4.6. Circle with center C, radius r

🔗

Observe that a circle is symmetric with respect its center. Based on the definition, a point P is on the circle if and only if its distance to C is r, that is |CP| = r. A point in the plane is said to be inside the circle if its distance to the center C is less than r. Similarly, a point in the plane is said to be outside the circle if its distance to C is greater than r. Moreover, a chord of the circle is a line segment whose endpoints are on the circle. A diameter is a chord of the circle through the center C. Consequently, C is the midpoint of a diameter and the length of a diameter is 2r. For example, AB and QR are diameters of the circle in Figure 4.6.

🔗

Example 4.2.2.

Consider a circle of radius 5 whose center is at C(2,1). Determine whether each of the following points is on the circle, inside the circle or outside the circle:

🔗

\(P_1(5, 5), P_2(4, 5), P_3(−2, 5), P_4(−1, −2), P_5(2,−4), P_6(7, 0).\)

🔗

Solution.

The distance between a given point P(x,y) and the center C(2,1) is given by

🔗

\(|PC| = \sqrt{(x-2)^2+(y-1)^2}.\) or \(|PC|^2 = (x-2)^2+(y-1)^2\) We need to compare |PC| with the radius \(5\text{.}\)

🔗

Note that |PC| \(=5 ⇔ |PC|^2 = 25, \quad |PC|< 5 ⇔ |PC|^2< 25\) ,

🔗

and \(|PC| >5 ⇔ |PC|^2 > 25.\)

🔗

Thus, P is on the circle if \(|PC|^2 =25\text{,}\) inside the circle if |PC|\(^2 < 25\) and outside the circle if |PC|\(^2 > 25\text{.}\) So, we can use the square distance to answer the question. Thus, as

🔗

\(|P_1C|^2 = (5-2)^2+(5-1)^2 = 25, |P_2C|^2 = (4-2)^2+(5-1)^2= 20\)

🔗

and \(|P_3C|^2 = (-2-2)^2+(5-1)^2= 32,\)

🔗

\(P_1\) is on the circle, \(P_2\) is inside the circle, and \(P_3\) is outside the circle. Similarly, you can show that \(P_4\) is inside the circle, \(P_5\) is on the circle, and \(P_6\) is outside the circle.

🔗

Exercises Exercises

1.

Suppose the center of a circle is \(C(1,-2)\) and \(P(7, 6)\) is a point on the circle. What is the radius of the circle?

🔗

2.

Let \(A(1, 2)\) and \(B(5, -2)\) are endpoints of a diameter of a circle. Find the center and radius of the circle.

🔗

3.

Consider a circle whose center is the origin and radius is. Determine whether or not the circle contains the following point.

🔗

\(\displaystyle (1, 2) \)
🔗

🔗
\(\displaystyle (0,0)\)
🔗

🔗
\(\displaystyle (0, -\sqrt{5})\)
🔗

🔗
\(\displaystyle \left(\frac{3}{2}, \frac{3}{2}\right)\)
🔗

🔗
\(\displaystyle (5, 0)\)
🔗

🔗
\(\displaystyle (-1, -2)\)
🔗

🔗
\(\displaystyle (2, 4)\)
🔗

🔗
\(\displaystyle \left(\frac{5}{2}, \frac{5}{2}\right)\)
🔗

🔗

🔗

4.

Consider a circle of radius 5 whose center is at \(C(-3,4)\text{.}\) Determine whether each of the following points is on the circle, inside the circle or outside the circle:

🔗

\(\displaystyle (0, 9)\)
🔗

🔗
\(\displaystyle (0,0)\)
🔗

🔗
\(\displaystyle (1,6) \)
🔗

🔗
\(\displaystyle (1, 0)\)
🔗

🔗
\(\displaystyle (-7, 1)\)
🔗

🔗
\(\displaystyle (-1, -1)\)
🔗

🔗
\(\displaystyle (2,4)\)
🔗

🔗
\(\displaystyle \left(\frac{5}{2}, \frac{5}{2}\right)\)
🔗

🔗

🔗

Checkpoint 4.2.3.

Add review

docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FAnalytic-Geometry-%28NS%29%2FDefinition-of-a-circle%2FDetermining-Positions-of-Points-with-Respect-to-a-Given-Circle.xml&entry.2077830997=source%2Fanalytic-geometry%2Fsections%2Fsubsections%2Fsec-circles%2Fsubsec-definition-of-a-circle.ptx

🔗

Checkpoint 4.2.4.

Add review

docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FAnalytic-Geometry-%28NS%29%2FDefinition-of-a-circle%2FFinding-the-Center-and-Radius-of-a-Circle-Given-Endpoints-of-a-Diameter.xml&entry.2077830997=source%2Fanalytic-geometry%2Fsections%2Fsubsections%2Fsec-circles%2Fsubsec-definition-of-a-circle.ptx

🔗

Checkpoint 4.2.5.

Add review

docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FAnalytic-Geometry-%28NS%29%2FDefinition-of-a-circle%2FFinding-the-Radius-of-a-Circle-with-Given-Center-and-Point-on-the-Circumference.xml&entry.2077830997=source%2Fanalytic-geometry%2Fsections%2Fsubsections%2Fsec-circles%2Fsubsec-definition-of-a-circle.ptx

🔗

Subsection 4.2.2 Equation of a Circle

We now construct an equation that the coordinates (x,y) of the points on the circle should satisfy. So, let P(x,y) be any point on a circle of radius r and center C(h,k) (see, Figure 4.7).

🔗

Then, the definition of a circle requires that |CP|= r

🔗

\(\quad\quad ⇒ \sqrt{(x-h)^2 + (y-k)^2} = r\)

🔗

\(\quad\quad\quad (x-h)^2 + (y-k)^2 = r^2\)

🔗

(Standard equation of a circle with center (h,k) and radius r).

🔗

In particular, if the center is at origin, i.e., (h,k) = \((0,0)\text{,}\) the equation is

🔗

\(\quad\quad\quad x^2 + y^2 = r^2\)

🔗

(Standard Equation of a circle of radius r centered at origin)

🔗

Figure 4.7: Circles (a) Center at C(h,k) ; (b) Center at origin

🔗

Example 4.2.6.

Find an equation of the circle with radius \(4\) and center \((-2, 1)\text{.}\)

🔗

Solution.

Using the standard equation of a circle in which the center (h, k) = \((-2, 1)\) and radius r = \(4\text{,}\)

🔗

we obtain the equation:

🔗

\((x+ 2)^2 + (y-1)^2 = 16\)

🔗

Example 4.2.7.

Find the equation of a circle with endpoints of a diameter at \(P(-2, 0)\) and \(Q(4, 2)\text{.}\)

🔗

Solution.

The center of the circle C(h,k) is the mid-point of the diameter.

🔗

Hence, \((h,k) = \left(\frac{-2+4}{2}, \frac{0+2}{2}\right) = (1,1)\text{.}\)

🔗

Also, for its radius r, \(r^2 = |CP|^2 =(1+2)^2+(1-0)^2 = 10\text{.}\)

🔗

Thus, the equation of the circle is \((x - h)^2+(y - k)^2 = r^2\text{.}\)

🔗

That is, \((x - 1)^2+(y -1)^2 = 10 \text{.}\)

🔗

Example 4.2.8.

Suppose \(P(-2,4)\) and \(Q(5,3)\) are points on a circle whose center is on x-axis. Find the equation of the circle.

🔗

Solution.

We need to obtain the center \(C\) and radius r of the circle to construct its equation.

🔗

As the center is on x-axis, its second coordinate is \(0\text{.}\)

🔗

Therefore, let C(h,0) be the center of the circle.

🔗

Note that \(|PC|^2 = |QC|^2 = r^2 \) as both \(P\) and \(Q\) are on the circle.

🔗

So, from the first equality we get \((-2-h)^2 + 4^2= (5-h)^2 + 3^2\) .

🔗

Solving this for h we get \(h=1\text{.}\)

🔗

Hence, the center is at \(C(1, 0)\) and \(r^2 = |QC|^2 = (5-1)^2 + 3^2 =25 \text{.}\)

🔗

Therefore, the equation of the circle is \((x - 1)^2 + y^2 = 25\text{.}\)

🔗

Example 4.2.9.

Determine whether the given equation represents a circle. If it does, identify its center and radius and sketch its graph.

🔗

\(\displaystyle x^2 + y^2 + 2x - 6y + 7 = 0\)
🔗

🔗
\(\displaystyle x^2 + y^2 + 2x - 6y + 10 = 0\)
🔗

🔗
\(\displaystyle x^2 + y^2 + 2x - 6y + 11 = 0\)
🔗

🔗

🔗

Solution.

We need to rewrite each equation in standard form to identify its center and radius.

🔗

We do this by completing the square on the x-terms and y-terms of the equation as follows:

🔗

\((x^2 + 2x) + (y^2 - 6y) = -7\)
🔗

(Grouping x-terms and y-terms)
🔗

🔗
\(⇔(x^2+2x+1^2)+ (y^2-6y+3^2) = -7+1+9.\)
🔗

(Adding \(1^2\) and \(3^2\) to both sides)
🔗

\(⇔ ( x + 1)^2 + (y - 3)^2 = 3\text{.}\)
🔗

Comparing this with the standard equation of a circle, this is the equation of a circle with center (h, k) = (-1, 3) and radius r = \(\sqrt{3}\text{.}\)
🔗

The graph of the circle is sketched in Figure 4.8 below.
🔗

Figure 4.8.
🔗

🔗
Following the same steps as in (a), you can see that \(x^2 + y^2 + 2x - 6y +10 = 0\) is equivalent to \((x + 1)^2 + (y- 3)^2 = 0\text{.}\)
🔗

This is satisfied by the point \((-1, 3)\) only. The locus of this equation is considered as a point-circle, circle of zero radius (sometimes called degenerated circle).
🔗

🔗
Again following the same steps as in (a), you can see that \(x^2 + y^2 + 2x - 6y +11 = 0\) is equivalent to \((x + 1)^2 + (y - 3)^2 = -1\text{.}\)
🔗

Note that this does not represent a circle; in fact it has no locus at all (Why? ).
🔗

🔗

🔗

Remark 4.2.10.

🔗

Consider an equation of the form

🔗

\begin{equation*} x^2 + y^2 + Dx + Ey + F = 0 \end{equation*}

By completing the square you can show the following:

🔗

If \(D^2 + E^2 - 4F > 0\) , then the equation represents a circle with center \(\left(-\frac{D}{2}, -\frac{E}{2}\right)\) and radius \(r = \frac{1}{2}\sqrt{D^2 + E^2 - 4F}\text{.}\)
🔗

🔗
If \(D^2 + E^2 - 4F = 0\) , then the equation is satisfied by the point \(\left(-\frac{D}{2}, -\frac{E}{2}\right)\) only. In this case the locus of the equation is called point-circle (circle of zero radius).
🔗

🔗
If \(D^2 + E^2 - 4F < 0\) , then the equation has no locus.
🔗

🔗

🔗

Exercises Exercise

1.

Determine whether each of the following points is inside, outside or on the circle with equation \(x^2+y^2=5\text{.}\)

🔗

\(\displaystyle (-1, 2)\)
🔗

🔗
\(\displaystyle \left(\frac{3}{2}, 2 \right) \)
🔗

🔗
\(\displaystyle (0,-\sqrt{5})\)
🔗

🔗
\(\displaystyle \left(-1, \frac{3}{2} \right)\)
🔗

🔗

🔗

2.

Find an equation of the circle whose endpoints of a diameter are \((0, −3)\) and \((3, 3)\text{.}\)

🔗

3.

Determine an equation of a circle whose center is on y-axis and radius is \(2\text{.}\)

🔗

4.

Find an equation of the circle passing through \((1, 0)\) and \((0, 1)\) which has its center on the line \(2x + 2y =5\text{.}\)

🔗

5.

Find the value(s) of k for which the equation \(2x^2 + 2y^2 + 6x - 4y + k =0\) represent a circle.

🔗

6.

An equation of a circle is \(x^2+ y^2-6y + k=0\text{.}\) If the radius of the circle is \(2\text{,}\) then what is the coordinates of its center?

🔗

7.

Find equation of the circle passing through \((0,0), (4, 0)\) and \((2, 2)\text{.}\)

🔗

8.

Find equation of the circle inscribed in the triangle with vertices (\(-7, -10), (-7, 15)\text{,}\) and \((5,-1)\text{.}\)

🔗

9.

In each of the following, check whether or not the given equation represents a circle. If the equation represents a circle, then identify its center and the length of its diameter.

🔗

\(\displaystyle x^2+y^2-18x +24y = 0\)
🔗

🔗
\(\displaystyle x^2+y^2-2x+4y+5=0\)
🔗

🔗
\(\displaystyle x^2+y^2-4x-2y+11=0\)
🔗

🔗
\(\displaystyle 5x^2 + 5y^2+125x+60y-100=0\)
🔗

🔗
\(\displaystyle 36x^2+36y^2+12x+24y-139=0\)
🔗

🔗
\(\displaystyle 3x^2 + 3y^2 + 2x+4y+6=0\)
🔗

🔗

🔗

10.

Show that \(x^2 + y^2 + Dx + Ey + F = 0\) represents a circle of positive radius iff \(D^2 + E^2- 4F > 0\text{.}\)

🔗

Checkpoint 4.2.11.

Add review

⁴

docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FAnalytic-Geometry-%28NS%29%2FEquation-of-a-circle%2FFinding-the-Standard-Form-of-Circle-Equation-with-Given-Center-and-Point.xml&entry.2077830997=source%2Fanalytic-geometry%2Fsections%2Fsubsections%2Fsec-circles%2Fsubsec-equation-of-a-circle.ptx

🔗

Checkpoint 4.2.12.

Add review

⁵

docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FAnalytic-Geometry-%28NS%29%2FEquation-of-a-circle%2FCircle-Equation-with-Center-on-a-Given-Line.xml&entry.2077830997=source%2Fanalytic-geometry%2Fsections%2Fsubsections%2Fsec-circles%2Fsubsec-equation-of-a-circle.ptx

🔗

Checkpoint 4.2.13.

Add review

⁶

docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FAnalytic-Geometry-%28NS%29%2FEquation-of-a-circle%2FEquation-of-a-Circle-with-Given-Center-and-Radius.xml&entry.2077830997=source%2Fanalytic-geometry%2Fsections%2Fsubsections%2Fsec-circles%2Fsubsec-equation-of-a-circle.ptx

🔗

Subsection 4.2.3 Intersection of a circle with a line and tangent line to a circle

The number of intersection points of a given line and a circle is at most two; that is, either no intersection point, or only one intersection point, or two intersection points. For instance, in Figure 4.9, the line \(l_1\) has no intersection with the circle, \(l_2 \) has two intersection points with the circle, namely, \(Q_1\) and \(Q_2\text{,}\) and \(l_3\) has only one intersection point with the circle, namely, P.

🔗

A line which intersects a circle at one and only one point is called a tangent line to the circle. In this case, the intersection point is called the point of tangency. Thus, \(l_3 \) a tangent line to the circle in Figure 4.9 and P is the point of tangency.

🔗

Figure 4.9. Intersection of a line and circle

🔗

In Figure 4.9, observe that every point on \(l_1\) are outside of the circle. Hence, d(C,Q) > r for every point Q on \(l_1\text{.}\) Consequently, \(d(C, l_1) > r\text{.}\) On the other hand, there is a point on \(l_2\) which is inside the circle. Hence, \(d(C, l_2) < r\)

🔗

For the tangent line \(l_3 \) the point of tangency P is on the circle implies that \(|CP| = r\) and P is the point on \(l_3 \)closest to C. Therefore, \(d(C, l) = |CP|= r\text{.}\) This shows also that CP⊥ \(l_3\text{.}\)

🔗

In general, given a circle of radius r with center C(h,k) and a line l , by computing the distance d(C, l) between C and l we can conclude the following.

🔗

If d(C, l) > r, then the line does not intersect with the circle.
🔗

🔗
If d(C, l) < r, then the line is a secant of the circle; that is, they have two intersection points.
🔗

🔗
If d(C, l) = r, then l is a tangent line to the circle. The point of tangency is the point P on the line (and on the circle) such that CP ⊥ l . This means the product of the slopes of l and CP must be \(-1\text{.}\)
🔗

🔗

🔗

Example 4.2.14.

Write the equation of the circle tangent to the x-axis at \((6,0)\) whose center is on the line \(x-2y = 0\text{.}\)

🔗

Solution.

The circle in the question is as in Figure 4.10.

🔗

Figure 4.10

🔗

Let C(h, k) be the center of the circle.

🔗

(h, k) is on the line \(y = \left(\frac{1}{2}\right)x ⇒ k = \left(\frac{1}{2} \right)h\) ; and the circle is tangent to x-axis at P\((6,0) ⇒ \)CP should be perpendicular to the x-axis.

🔗

\(⇒ h = 6 ⇒ k= 3\) and the radius is r \(= |CP| = k-0 =3\text{.}\)

🔗

Hence, the circle is centered at \((6, 3)\) with radius r \(=3\text{.}\)

🔗

Therefore, the equation of the circle is \((x - 6)^2 + (y-3)^2 = 9\) .

🔗

Example 4.2.15.

Suppose the line y=x is tangent to a circle at point P\((2,2)\text{.}\) If the center of the circle is on the x-axis, then what is the equation of the circle?

🔗

Solution.

The circle in the question is as in Figure 4.11.

🔗

Figure 4.11.

🔗

Let the center of the circle be C(h,0). We need to find h.

🔗

The slope of the line l : y=x is \(1\) and l is perpendicular to CP.

🔗

Hence the slope of CP is \(-1\text{.}\)

🔗

So, the slope of CP \(= \frac{2-0}{2-h} = -1 ⇒ h-2=2\) or \(h=4\text{.}\)

🔗

\(⇒ \)The center of the circle is C\((4,0)\text{;}\) and \(r^2 = |CP|^2 = (2-0)^2 + (2 - 4)^2 = 4+4= 8.\)

🔗

Therefore, the equation of the circle is \((x - 4)^2 + y^2= r^2 = 8\text{.}\)

🔗

Exercises Exercise

1.

Find the equation of the line tangent to the circle with the center at \((-1, 1)\) and point of tangency at \((-1, 3)\text{.}\)

🔗

2.

The center of a circle is on the line \(y =2x\) and the line \(x=1\) is tangent to the circle at \((1, 6)\text{.}\) Find the center and radius of the circle.

🔗

3.

Suppose two lines \(y = x\) and \(y = x - 4\) are tangent to a circle at \((2,2)\) and \((4,0)\text{,}\) respectively. Find the equation of the circle.

🔗

4.

Find an equation of the line tangent to the circle \(x^2 + y^2 - 2x +2y = 2\) at \((1,1)\)

🔗

5.

Find equation of the line through (\(\sqrt{32},0\)) and tangent to the circle with equation \(x^2 + y^2 = 16\text{.}\)

🔗

6.

Suppose P(\(1,2\)) and Q(\(3, 0\)) are the endpoints of a diameter of a circle and L is the line tangent to the circle at Q.

Show that R(\(5, 2\)) is on L.

🔗
Find the area of ∆PQR, when R is the point given in (a).

🔗

🔗

Checkpoint 4.2.16.

Add review

⁷

docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FAnalytic-Geometry-%28NS%29%2FIntersection-of-a-circle-with-a-line-and-tangent-line-to-a-circle%2FFinding-Points-of-Intersection-between-a-Circle-and-a-Line.xml&entry.2077830997=source%2Fanalytic-geometry%2Fsections%2Fsubsections%2Fsec-circles%2Fsubsec-intersection-of-a-circle-with.ptx

🔗

Checkpoint 4.2.17.

Add review

⁸

docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FAnalytic-Geometry-%28NS%29%2FIntersection-of-a-circle-with-a-line-and-tangent-line-to-a-circle%2FTangent-Line-and-Circle-with-x-axis-Center.xml&entry.2077830997=source%2Fanalytic-geometry%2Fsections%2Fsubsections%2Fsec-circles%2Fsubsec-intersection-of-a-circle-with.ptx

🔗

Prev Top Next