Skip to main content

BASIC MATHEMATICS FOR NATURAL SCIENCES UNDERGRADUATE STUDENT TEXTBOOK

Ato Arbsie Yasin, Dr. Berhanu Bekele, Dr. Berhanu Guta, Ato Wondwosen Zemene

Section 1.4 Set theory

Subsection 1.4.1 The concept of a set

The term set is an undefined term, just as a point and a line are undefined terms in geometry. However, the concept of a set permeates every aspect of mathematics. Set theory underlies the language and concepts of modern mathematics. The term set refers to a well-defined collection of objects that share a certain property or certain properties. The term “well-defined” here means that the set is described in such a way that one can decide whether or not a given object belongs in the set. If \(A\) is a set, then the objects of the collection \(A\) are called the elements or members of the set \(A\text{.}\) If \(x\) is an element of the set \(A\text{,}\) we write \(x \in A\text{.}\) If \(x\) is not an element of the set \(A\text{,}\) we write \(x \notin A\text{.}\)
🔗
As a convention, we use capital letters to denote the names of sets and lowercase letters for elements of a set.
🔗
Note that for each objects \(x\) and each set \(A\text{,}\) exactly one of \(\text{x } \in A\) or \(\text{x } \notin A\) but not both must be true.
🔗

Checkpoint 1.4.1.

Add review
 1 
docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FPropositional-Logic-and-Set-Theory-%28NS-and-SS%29%2FThe-concept-of-a-set%2FRelationship-between-elements-and-sets-notation.xml&entry.2077830997=source%2Fpropositional-logic-and-set-theory%2Fsections%2Fsubsections%2Fsec-set-theory%2Fsubsec-the-concept-of-a-set.ptx
🔗

Checkpoint 1.4.2.

Add review
 2 
docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FPropositional-Logic-and-Set-Theory-%28NS-and-SS%29%2FThe-concept-of-a-set%2FIntroduction-to-sets-and-set-notation.xml&entry.2077830997=source%2Fpropositional-logic-and-set-theory%2Fsections%2Fsubsections%2Fsec-set-theory%2Fsubsec-the-concept-of-a-set.ptx
🔗
🔗

Subsection 1.4.2 Description of Sets

Sets are described or characterized by one of the following four different ways.
🔗
\(\textbf{1. Verbal Method}\)
🔗
In this method, an ordinary English statement with minimum mathematical symbolization of the property of the elements is used to describe a set. actually, the statement could be in any language.
🔗

Example 1.4.3.

  1. The set of counting numbers less than ten.
    🔗
    🔗
  2. The set of letters in the word “Addis Ababa.”
    🔗
    🔗
  3. The set of all countries in Africa.
    🔗
    🔗
🔗
🔗
\(\textbf{2. Roster/Complete Listing Method}\)
🔗
If the elements of a set can be listed, we list them all between a pair of braces without repetion separating by commas, and without concern about the order of their appearance. Such a method of describing a set is called the rooster/complete listing method.
🔗

Example 1.4.4.

  1. The set of vowels in English alphabet may also be desribed as \(\left\{a, e, i, o, u\right\}.\)
    🔗
    🔗
  2. The set of positive factors of \(24\) is also described as \(\left\{1, 2, 3, 4, 6, 8, 12, 24\right\}.\)
    🔗
    🔗
🔗
🔗

Remark 1.4.5.

  1. We agree on the convention that the order of writing the elements in the list is immaterial. As a result the sets \(\left\{ a, b, \left\{ c\right\}\right\},\, \left\{ b, c, a\right\} \text{ and } \left\{ c, a, b\right\}\) contain the same elements, namely \(a, b \text{ and } c.\)
    🔗
    🔗
  2. The set \(\left\{a, a, b, b\right\}\) contains just two distinct elements; namely \(a \text{ and } b,\) hence it is the same set as \(\left\{a, b\right\}.\) We list distinct elements without repetition.
    🔗
    🔗
🔗
🔗

Example 1.4.6.

  1. Let \(A = \left\{a, b,\left\{c\right\}\right\}.\) Elements of \(A\) are \(a, b \text{ and } {c}.\)
    🔗
    Notice that \(c \text{ and } \left\{c\right\}\) are different objects. Here \(\left\{c\right\} \in A\) but \(c \notin A.\)
    🔗
    🔗
  2. Let \(B = \left\{\left\{a\right\}\right\}.\) The only element of \(B\) is \(\left\{a\right\}.\) But \(a \notin B.\)
    🔗
    🔗
  3. Let \(C = \left\{a, b, \left\{a, b\right\}, \left\{a, \left\{a\right\}\right\}\right\}.\) Then \(C\) has four elements.
    🔗
    🔗
🔗
The readers are invited to write down all the elements of \(C.\)
🔗
🔗
\(\textbf{3. Partial Listing Method}\)
🔗
In many occassions, the number of elements of a set may be too large to list them all; and in other occassions there may not be an end to the list. In such cases we look for a common property of the elements and describe the set by partially listing the elements. More precisely, if the common property is simple that it can easily be identified from a list of the first few elements, then within a pair of braces, we list these few elements followed (or preceded) by exactly three dotes and possibly by one last element. The following are such instances of describing sets by partial listing method.
🔗

Example 1.4.7.

  1. The set of all counting numbers in \(\mathbb{N} = \left\{1, 2, 3, 4, ...\right\}.\)
    🔗
    🔗
  2. The set of non-positive integers is \(\left\{..., -4, -3, -2, -1, 0, ...\right\}.\)
    🔗
    🔗
  3. The set of multiples of \(5\) is \(\left\{..., -15, -10, -5, 0, 5, 10, 15, ...\right\}.\)
    🔗
    🔗
  4. The set of odd integers less than \(100\) is \(\left\{..., -3, -1, 1, 3, 5, ... 99\right\}.\)
    🔗
    🔗
🔗
🔗
\(\textbf{4. Set-builder Method}\)
🔗
When all the elements satisfy a common property \(P,\) we express the situation as an open proposition \(P(x)\) and describe the set using a method called the set-builder Method as follows:
🔗
\(A = \left\{x | P(x)\right\} or A = \left\{x: P(x)\right\}\)
🔗
We read it as “\(A\) is equal to the set of all \(x\)’s is true.” Here the bar “|” and the colon “:” mean “such that.” Notice that the letter \(x\) is only a place holder and can be replaced throughout by other letters. So, for a property \(P,\) the set \(\left\{x | P(x)\right\},\, \left\{t | P(t)\right\} \text{ and } \left\{y | P(y)\right\}\) are all the same set.
🔗

Example 1.4.8.

The following sets are described using the set-builder method.
🔗
  1. \(\displaystyle A = \left\{x | x \text{ is a vowel in the English alphabet}\right\}.\)
    🔗
    🔗
  2. \(\displaystyle B = \left\{t | t \text{ is an integer}\right\}.\)
    🔗
    🔗
  3. \(\displaystyle C = \left\{n | n \text{is an natural number and } 2n-15 \text{ is negative}\right\}.\)
    🔗
    🔗
  4. \(\displaystyle D = \left\{y | y^2 - y -6 = 0\right\}.\)
    🔗
    🔗
  5. \(\displaystyle E = \left\{x | x \text{ is an integer and } x - 1 < 0 \Rightarrow x^2 - 4 > 0 \right\}.\)
    🔗
    🔗
🔗
🔗

Checkpoint 1.4.9.

Express each of the above by using either the complete or the oartial listing method.
🔗
🔗

Definition 1.4.10.

The set which has no elements is called the empty (or null) set and is denoted by \(\phi \text{ or} \left\{\right\}\)
🔗
🔗

Example 1.4.11.

The set of \(x \in \mathbb{R}\) such that \(x^2 + 1 = 0\) is an empty set.
🔗
🔗

Definition 1.4.12.

A set is finite if it has limited number of elements and it is called infinite if it unlimited number of elements.
🔗
🔗
\(\textbf{Relationship between two sets}\)
🔗

Definition 1.4.13.

Set \(B\) is said to be a subset of set \(A\) (or is contained in \(A\)), denoted by \(B \subseteq A,\) every element of \(B\) is an element of \(A,\) i.e.,
\begin{equation*} (\forall x) (x\in B\Rightarrow x\in A). \end{equation*}
🔗
It follows from the definition that set \(B\) is not a subset of set \(A\) if at least one element of \(B\) is not an element of \(A.\) i.e., \(B\notin A\Leftrightarrow (\exists x)(x\in B\Rightarrow x\notin A).\) In such cases we write \(B\nsubseteq A\) or \(A\nsupseteq B.\)
🔗
🔗

Remark 1.4.14.

For any set \(A, \phi \subseteq A \) and \(A \subseteq A.\)
🔗
🔗

Example 1.4.15.

  1. If \(A = \left\{a, b\right\},\, B = \left\{a, b, c\right\} \text{ and } C = \left\{a, b, d\right\}\) then \(A \subseteq B\) and \(A \subseteq C.\) On the other hand, it is clear that \(B \nsubseteq A,\, B \nsubseteq C \) and \(C \nsubseteq B.\)
    🔗
    🔗
  2. If \(S = \left\{x | x \text{ is a multiple of } 6 \right\}\) and \(T = \left\{x | x \text{ is even integer }\right\},\) then \(S \subseteq T\) since every multiple of \(6\) is even. However, \(2 \subseteq T\) while \(2 \nsubseteq S.\) Thus \(T \nsubseteq S.\)
    🔗
    🔗
  3. If \(A = \left\{a, \left\{b\right\}\right\}\) then \(\left\{a\right\}\subseteq A\) and \(\left\{\left\{b\right\}\right\} \subseteq A.\) On the other hand, since \(b \notin A, \, \left\{b\right\} \nsubseteq A\) and \(\left\{a, b\right\} \nsubseteq A.\)
    🔗
    🔗
🔗
🔗

Definition 1.4.16.

  1. Sets \(A\) and \(B\) are said to be equal if they contain exactly the same elements. In this case, we write
    \begin{equation*} A = B. \text{That is, } (\forall x) (x\in B\Rightarrow x\in A). \end{equation*}
    🔗
    🔗
  2. Sets \(A\) and \(B\) are said to be equivalent if and only if there is a one to one correspondence among their elements. In this case, we write \(A\leftrightarrow B.\)
    🔗
    🔗
🔗
🔗

Example 1.4.17.

  1. The sets \(\left\{1, 2, 3\right\},\, \left\{2, 1, 3\right\}, \, \left\{1, 3, 2\right\}\) are all equal.
    🔗
    🔗
  2. \(\displaystyle \left\{x | x \text{ is a counting number }\right\} = \left\{x | x \text{ is a positive inetger }\right\}\)
    🔗
    🔗
🔗
🔗

Definition 1.4.18.

The set \(A\) is said to be a proper subset of \(B\) if every element \(A\) is also an element in \(B,\) but \(B\) has at least one element that is not in \(A.\) In this case, we write \(A\subset B.\) We also say \(B\) is a proper set of \(A,\) and write \(B\supset A.\) It is clear that
\begin{equation*} A\subset B\Leftrightarrow \left [ \left ( \forall x \right ) \left ( x\in A\Rightarrow x\in B \right )\wedge \left ( A\neq B \right )\right ] \end{equation*}
🔗
🔗

Remark 1.4.19.

Some authors do not use the symbol \(\subseteq.\) Instead they use the symbol \(\subset\) for both subset and proper subset. In this material, we prefer to use the notations commonly used in highschool mathematics, and we continue using \(\subseteq\) and \(\subset\) differently, namely for subset and proper subset, respectively.
🔗
🔗

Definition 1.4.20.

Let \(A\) be a set. The power set of \(A,\) denoted by \(P\left ( A \right ),\) is the set whose elements are all subsets of \(A.\) That is,
\begin{equation*} P\left ( A \right )= \left\{ B:B\subseteq A\right\}. \end{equation*}
🔗
🔗

Note 1.4.21.

If a set \(A\) is finite with \(n\) elements, then
  1. The number of subsets of \(A\) is \(2^n\) and
    🔗
    🔗
  2. The number of proper subsets of \(A\) is \(2^n - 1.\)
    🔗
    🔗
🔗
🔗

Example 1.4.22.

Let \(A = \left\{ x, y, z\right\}.\) As denoted before, \(\phi\) and \(A\) are subset af \(A.\) Moreover, \(\left\{ x\right\},\left\{ y\right\}, \left\{ z\right\}, \left\{ x, y\right\}, \left\{ x, z\right\}\text{ and } \left\{ y, z\right\}\) are all subsets of \(A.\) Therefore,
\begin{equation*} P\left ( A \right )=\left\{ \phi, \left\{ x\right\},\left\{ y\right\}, \left\{ z\right\}, \left\{ x, y\right\}, \left\{ x, z\right\}, \left\{ y, z\right\}, A\right\} \end{equation*}
🔗
🔗
Frequently it is necessary to limit the topic of discussion to elements of a certain fixed set and regard all sets under consideration as a subset of this fixed set. We call this set the universal set or the universe and denoted by U.
🔗

Exercises Exercises

1.
Which of the following are sets?
  1. \(\displaystyle 1, 2, 3\)
    🔗
    🔗
  2. \(\displaystyle \left\{1, 2 \right\}, 3\)
    🔗
    🔗
  3. \(\displaystyle \left\{ \left\{ 1,\right\} 2\right\}, 3\)
    🔗
    🔗
  4. \(\displaystyle \left\{1 \left\{ 2\right\},3\right\}\)
    🔗
    🔗
  5. \(\displaystyle \left\{1, 2, a, b\right\}.\)
    🔗
    🔗
🔗
🔗
2.
Which of the following sets can be described in complete listing, partial listing and/or set-builder methods? Describe each set by at least one of the three methods.
  1. The set of the first \(10\) letters in the English alphabet.
    🔗
    🔗
  2. The set of all countries in the world.
    🔗
    🔗
  3. The set of students of Addis Ababa University in the 2018/2019 academic year.
    🔗
    🔗
  4. The set of positive multiples of \(5.\)
    🔗
    🔗
  5. The set of all horses with six legs.
    🔗
    🔗
🔗
🔗
3.
Write each of the following sets by listing its elements within braces.
  1. \(\displaystyle A=\left\{ x\in \mathbb{Z}:-4 <x\leq 4\right\}\)
    🔗
    🔗
  2. \(\displaystyle B=\left\{ x\in \mathbb{Z}:x^2 < 5 \right\}\)
    🔗
    🔗
  3. \(\displaystyle C=\left\{ x\in \mathbb{N}:x^3 < 5 \right\}\)
    🔗
    🔗
  4. \(\displaystyle D=\left\{ x\in \mathbb{R}:x^2 -x = 0 \right\}\)
    🔗
    🔗
  5. \(\displaystyle D=\left\{ x\in \mathbb{R}:x^2 + 1 = 0 \right\}.\)
    🔗
    🔗
🔗
🔗
4.
Let \(A\) be the set of positive even integers less than \(15.\) Find the truth value of each of the following.
  1. \(\displaystyle 15 \in A\)
    🔗
    🔗
  2. \(\displaystyle -16 \in A\)
    🔗
    🔗
  3. \(\displaystyle \phi \in A\)
    🔗
    🔗
  4. \(\displaystyle 12 \subset A\)
    🔗
    🔗
  5. \(\displaystyle \left\{ 2, 8, 14\right\} \in A\)
    🔗
    🔗
  6. \(\displaystyle \left\{ 2, 3, 4\right\} \subseteq A\)
    🔗
    🔗
  7. \(\displaystyle \left\{ 2, 4\right\} \in A\)
    🔗
    🔗
  8. \(\displaystyle \phi \subset A\)
    🔗
    🔗
  9. \(\displaystyle \left\{ 246\right\} \subseteq A\)
    🔗
    🔗
🔗
🔗
5.
Find the truth value of each of the following and verify your conclusion.
  1. \(\displaystyle \phi \subseteq \phi\)
    🔗
    🔗
  2. \(\displaystyle \left\{ 1,2\right\}\subseteq \left\{ 1,2\right\}\)
    🔗
    🔗
  3. \(\phi \in A\) for any set \(A\)
    🔗
    🔗
  4. \(\left\{ \phi \right\}\subseteq A\) for any set \(A\)
    🔗
    🔗
  5. \(\displaystyle 5, 7 \subseteq \left\{ 5, 6, 7, 8\right\}\)
    🔗
    🔗
  6. \(\displaystyle \phi \in \left\{ \left\{ \phi \right\}\right\}\)
    🔗
    🔗
  7. For any set \(A, A \subset A\)
    🔗
    🔗
  8. \(\displaystyle \left\{ \left\{ \phi \right\}\right\} = \phi\)
    🔗
    🔗
🔗
🔗
6.
For each of the following set, find its power set.
  1. \(\displaystyle \left\{ ab\right\}\)
    🔗
    🔗
  2. \(\displaystyle \left\{ 1, 1.5\right\}\)
    🔗
    🔗
  3. \(\displaystyle \left\{ a, b\right\}\)
    🔗
    🔗
  4. \(\displaystyle \left\{ a, 0.5, x\right\}\)
    🔗
    🔗
🔗
🔗
7.
How many subsets and proper subsets do the sets that contain exactly \(1, 2, 3, 4, 8, 10 \text{ and } 20\) elements have?
🔗
🔗
10.
Find the truth value of each of the following.
  1. \(\displaystyle \phi \in P\left ( \phi \right )\)
    🔗
    🔗
  2. For any set \(A, \phi \subseteq P\left ( A \right )\)
    🔗
    🔗
  3. For any set \(A, A \in P\left ( A \right )\)
    🔗
    🔗
  4. For any set \(A, A \subset P\left ( A \right ).\)
    🔗
    🔗
🔗
🔗
11.
For any three sets \(A, B \text{ and } C,\) prove that:
  1. If \(A\subseteq B\) and \(B\subseteq C,\) then \(A\subseteq C.\)
    🔗
    🔗
  2. If \(A\subset B\) and \(B\subset C,\) then \(A\subset C.\)
    🔗
    🔗
🔗
🔗
🔗

Checkpoint 1.4.23.

Add review
 3 
docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FPropositional-Logic-and-Set-Theory-%28NS-and-SS%29%2FDescription-of-sets%2FFind-the-cardinality-of-the-largest-possible-set.xml&entry.2077830997=source%2Fpropositional-logic-and-set-theory%2Fsections%2Fsubsections%2Fsec-set-theory%2Fsubsec-description-of-sets.ptx
🔗

Checkpoint 1.4.24.

Add review
 4 
docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FPropositional-Logic-and-Set-Theory-%28NS-and-SS%29%2FDescription-of-sets%2FSet-Operations-and-Cardinality-Calculations-in-Set-Theory.xml&entry.2077830997=source%2Fpropositional-logic-and-set-theory%2Fsections%2Fsubsections%2Fsec-set-theory%2Fsubsec-description-of-sets.ptx
🔗

Checkpoint 1.4.25.

Add review
 5 
docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FPropositional-Logic-and-Set-Theory-%28NS-and-SS%29%2FDescription-of-sets%2FSet-Definition-and-Statement-Evaluation.xml&entry.2077830997=source%2Fpropositional-logic-and-set-theory%2Fsections%2Fsubsections%2Fsec-set-theory%2Fsubsec-description-of-sets.ptx
🔗

Checkpoint 1.4.26.

Add review
 6 
docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FPropositional-Logic-and-Set-Theory-%28NS-and-SS%29%2FDescription-of-sets%2FSet-Operations-and-Complements-with-Given-Sets-and-a-Universal-Set.xml&entry.2077830997=source%2Fpropositional-logic-and-set-theory%2Fsections%2Fsubsections%2Fsec-set-theory%2Fsubsec-description-of-sets.ptx
🔗
🔗

Subsection 1.4.3 Set Operations and Venn diagrams

Given two subsets \(A\) and \(B\) of a universal set \(U\text{,}\) new sets can be formed using \(A\) and \(B\) in many ways, such as taking common elements or non-common elements, and putting everything together. Such processes of forming new sets are called set operations. In this section, three most important operations, namely union, intersection and complement are discussed.
🔗

Definition 1.4.27.

The union of two sets \(A\) and \(B\text{,}\) denoted by \(A\cup B\text{,}\) is the set of all elements that are either in \(A\) or in \(B\)(or in both sets). That is,
\begin{equation*} A\cup B=\left\{ x:\left ( x\in A \right ) \vee \left ( x\in B \right )\right\} \end{equation*}
🔗
🔗
As easily seen the union operator “\(\cup\)” in the theory of set is the counterpart of the logical operator “\(\vee\)”
🔗

Definition 1.4.28.

The intersection of two sets \(A\) and \(B\text{,}\) denoted by \(A\cap B\text{,}\) is the set of all elements that are in \(A \text{ and } B.\) That is,
\begin{equation*} A\cap B=\left\{ x:\left ( x\in A \right ) \wedge \left ( x\in B \right )\right\} \end{equation*}
🔗
🔗
As suggested by Definition 1.4.28, the intersection operator “\(\cap\)” in the theory of sets is the counterpart of the logical operator “\(\wedge\)”.
🔗

Note 1.4.29.

Two sets \(A\) and \(B\) are said to be disjoint sets if \(A\cap B=\phi .\)
🔗
🔗

Example 1.4.30.

  1. Let \(A=\left\{ 0, 1, 3, 5, 6\right\} \text{ and } B=\left\{ 1, 2, 3, 4, 6, 7\right\}.\) Then,
    🔗
    \(A\cup B=\left\{ 0, 1, 2, 3, 4, 5, 6, 7\right\} \text{ and } A\cap B=\left\{ 1, 3, 6\right\}.\)
    🔗
    🔗
  2. Let \(A = \) The set of positive even integers and \(B = \) The set of positive multiples of 3. Then,
    🔗
    \(A\cup B=\left\{ x : x \text{ is a positive integer that is either even or a multiple of } 3 \right\}\)
    🔗
    \(\qquad = \left\{ 2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, ...\right\}\)
    🔗
    \(A\cap B=\left\{ x|x\text{ is a positive integer that is both even and a multiple of } 3\right\}\)
    🔗
    \(\qquad = \left\{ 6, 12, 18, 24, ...\right\}\)
    🔗
    \(\qquad = \left\{ x|x \text{ is a positive multiple of} 6.\right\}\)
    🔗
    🔗
🔗
🔗

Definition 1.4.31.

The difference between two sets \(A \text{ and } B,\) denoted by \(A - B,\) is all the elements in \(A\) and not in \(B;\) this set is also called the relative complement of \(B\) with respect to \(A.\) Symbolically,
\begin{equation*} A- B=\left\{ x:x\in A\wedge x\notin B\right\} \end{equation*}
🔗
🔗

Note 1.4.32.

\(A - B\) is sometimes denoted by \(A\setminus B.\) \(A-B \text{ and } A\setminus B\) are used interchangeably.
🔗
🔗

Example 1.4.33.

If \(A=\left\{1, 3, 5 \right\}, \, B=\left\{1, 2\right\},\) then \(A -B =\left\{ 3, 5 \right\}\) and \(B - A =\left\{ 2 \right\}.\)
🔗
🔗

Note 1.4.34.

The above example shows that, in general, \(A - B \text{ and } B - A\) are disjoint.
🔗
🔗

Definition 1.4.35.

Let \(A\) be a subset of a universal set \(U.\) The absolute complement (or simply complement) of \(A, \) denoted by \(A'(\text{ or }{A}^c \text{ or } \overline{A}),\) is defined to be the set of all elements of \(U\) that are not in \(A.\) That is,
\begin{equation*} A'= \left\{x:x\in U\wedge x\notin A \right\} \text{ or } A'\Leftrightarrow x\notin A\Leftrightarrow \neg \left ( x\in A \right ) \end{equation*}
🔗
🔗
Notice that taking the absolute complement of \(A\) is the same as finding the relative complement of \(A\) with respect to the universal set \(U.\) That is
\begin{equation*} A' = U - A. \end{equation*}
🔗

Example 1.4.36.

  1. If \(U=\left\{ 0, 1, 2, 3, 4\right\}\) and if \(A=\left\{ 3, 4\right\},\) then \(A' =\left\{ 0, 1, 2\right\}.\)
    🔗
    🔗
  2. \(U=\left\{ 1, 2, 3, ..., 12\right\}\)
    🔗
    \(A = \left\{ x|x \text{ is a positive factor of} 12\right\} \) and
    🔗
    \(B = \left\{ x|x \text{ is an odd integer of } U\right\}. \)
    🔗
    Then, \(A'=\left\{ 5, 7, 8, 9, 10, 11\right\}, \, \) \(B'=\left\{ 2, 4, 6, 8, 10, 12\right\},\)
    🔗
    \(\left ( A\cup B \right )'=\left\{ 8, 10\right\},\, A'\cup B' = \left\{ 2, 4, 5, 6, ..., 12\right\},\)
    🔗
    \(\left ( A\cap B \right )'=\left\{ 8, 10\right\}, \text{ and } \left ( A\setminus B\right )' = \left\{ 1, 3, 5, 7, 8, 9, 10, 11\right\}.\)
    🔗
    🔗
  3. Let \(U= \left\{ a, b, c, d, e , f, g, h \right\},\, A=\left\{ a, e, g, h\right\}\text{ and } B=\left\{ b, c, e, f, h\right\}.\) Then
    🔗
    \(A'=\left\{ b, c, d, f\right\}, \, B'=\left\{ a, d, g\right\}, B-A = \left\{ b, c, f\right\}\)
    🔗
    \(A-B=\left\{ a, g\right\}, \text{ and } \left ( A\cup B \right )'=\left\{ d\right\}\)
    🔗
    🔗
🔗
🔗
Find \(\left ( A\cap B \right )' ,\, A'\cap B', \, A'\cup B'.\) Which of these are equal?
🔗
Now we define the symmetric difference of two sets.
🔗

Definition 1.4.38.

The symmetric difference of two sets \(A \text{ and } B,\) denoted by \(A\Delta B,\) is the set
\begin{equation*} A\Delta B=\left ( A-B \right )\cup \left ( B-A \right ) \end{equation*}
🔗
🔗

Example 1.4.39.

Let \(U=\left\{1,2,3,...,10 \right\}\) be the universal set, \(A=\left\{2,4,6,8,9,10 \right\}\) and \(B=\left\{3,5,7,9 \right\}\) Then \(B-A=\left\{3,5,7 \right\}\) and \(A-B=\left\{2, 4, 6, 8, 10 \right\}.\) Thus \(A\Delta B=\left\{2, 3, 4, 5, 6, 7, 8, 10 \right\}.\)
🔗
🔗
Let us prove property “e” formally.
🔗
\(x\in A\cup (B\cap C)\) \(\Leftrightarrow \left ( x\in A \right )\vee \left ( x\in B\cap C \right )\) \(\left( \text{ definition of } \cup\right)\)
\(\Leftrightarrow x\in A \vee \left ( x\in B \wedge x\in C \right ) \) \(\left( \text{ definition of } \cap\right)\)
\(\Leftrightarrow \left ( x\in A \vee x\in B \right )\wedge\left(x\in A\vee x\in C \right ) \) \(\left(\vee \text{ is distributive over } \wedge \right)\)
\(\Leftrightarrow \left ( x\in A \cup B \right )\wedge\left(x\in A\cup C \right ) \) \(\left( \text{ definition of } \cup \right)\)
\(\Leftrightarrow x\in \left ( A \cup B \right )\cap\left(A\cup C \right )\) \(\left( \text{ definition of } \cap \right)\)
Therefore, we have \(A\cup \left ( B\cap C \right )=\left ( A\cup B \right )\cap \left ( A\cup C \right ).\)
🔗
The readers are invited to prove the rest part of the Theorem 1.4.40
🔗
\(\textbf{Venn diagrams}\)
🔗
While working with sets, it is helpful to use diagrams, called Venn diagrams, to illustrate the relationships involved. A Venn diagram is a schematic or pictorial representative of the sets involved in the discussion. Usually sets are represented as interlocking circles, each of which is enclosed in a rectangle, which represents the universal set \(U.\)
🔗
In some occasions, we list the elements of set \(A\) inside the curve representing A.
🔗

Example 1.4.41.

  1. If \(U=\left\{ 1,2,3,4,5,6,7\right\} \text{ and } A=\left\{ 2,4,6\right\},\) then a Venn diagram representation of these two sets looks like the following.
    🔗
    🔗
  2. Let \(U = \left\{ x|x \text{ is a positive integer less than} 13\right\}\)
    🔗
    \(A=\left\{ x|x\in U \text{ and } x \text{ is even} \right\}\)
    🔗
    \(B=\left\{ x|x\in U \text{ and } x \text{ is a multiple of } 3\right\}.\)
    🔗
    A Venn diagram representation of these sets is given below.
    🔗
    🔗
🔗
🔗

Example 1.4.42.

Let \(U = \text{The set of one digits numbers}\)
🔗
\(A = \) The set of one digits even numbers
🔗
\(B = \) The set of positive prime numbers less than 10
🔗
We illustrate the sets using a Venn diagram as follows.
🔗
  1. Illustrate \(A\cap B\) by a Venn diagram
    🔗
    🔗
  2. Illustrate \(A'\) by Venn diagram
    🔗
    🔗
  3. Illustrate \(A\setminus B\) by using a Venn diagram
    🔗
    🔗
🔗
🔗
Now we illustrate intersections and unions of sets by Venn diagram.
🔗

Exercises Exercises

1.
If \(B\subseteq A, \, A\cap B'= \left\{ 1,4,5\right\} \text{ and }A\cup B=\left\{ 1,2,3,4,5,6\right\}\) find \(B.\)
🔗
🔗
2.
Let \(A=\left\{ 2,4,6,7,8,9\right\}, \, B=\left\{ 1,3,5,6,10\right\}\) and \(C= \left\{x:3x+6=0 \text{ or } 2x+6=0\right\}.\) Find
  1. \(\displaystyle A\cup B\)
    🔗
    🔗
  2. Is \(\left ( A\cup B \right )\cup C=A\cup \left ( B\cup C \right )?\)
    🔗
    🔗
🔗
🔗
3.
Suppose \(U = \) The set of one digit numbers and \(A= \left\{ x:x \text{ is an even natural number less than or equal to } 9\right\}\)
🔗
Describe each of the sets by complete listing method:
  1. \(\displaystyle A'\)
    🔗
    🔗
  2. \(\displaystyle A \cap A'\)
    🔗
    🔗
  3. \(\displaystyle A \cup A'\)
    🔗
    🔗
  4. \(\displaystyle \left( A'\right)'\)
    🔗
    🔗
  5. \(\displaystyle \phi - U.\)
    🔗
    🔗
  6. \(\displaystyle \phi'\)
    🔗
    🔗
  7. \(\displaystyle U'\)
    🔗
    🔗
🔗
🔗
4.
Use Venn diagram to illustrate the following statements:
  1. \(\displaystyle \left ( A\cup B \right )'=A'\cap B'\)
    🔗
    🔗
  2. \(\displaystyle \left ( A\cap B \right )'=A'\cup B'\)
    🔗
    🔗
  3. \(\displaystyle A\nsubseteq B, \text{ then } A\setminus B\neq \phi \)
    🔗
    🔗
  4. \(\displaystyle A \cup A' = U\)
    🔗
    🔗
🔗
🔗
5.
Let \(A=\left\{ 1,2,3,4\right\}, \, B=\left\{ 5,7,8,9\right\} \text{ and } C=\left\{ 6,7,8\right\}.\) Then show that \(\left ( A\setminus B \right )\setminus C=A\setminus \left ( B\setminus C \right ).\)
🔗
🔗
6.
Perform each of the following operations
  1. \(\displaystyle \phi \cap \left\{ \phi \right\}\)
    🔗
    🔗
  2. \(\displaystyle \left\{ \phi , \left\{ \phi \right\}\right\}- \left\{ \left\{ \phi\right\}\right\}\)
    🔗
    🔗
  3. \(\displaystyle \left\{ \phi , \left\{ \phi \right\}\right\}- \left\{ \phi\right\}\)
    🔗
    🔗
  4. \(\displaystyle \left\{ \left\{ \left\{ \phi\right\}\right\}\right\}-\phi\)
    🔗
    🔗
🔗
🔗
7.
Let \(U=\left\{ 2,3,6,8,9,11,13,15\right\},\)
🔗
\(A=\left\{x|x \text{ is a positive prime factor of } 66\right\}\)
🔗
\(B=\left\{x\in U|x \text{ is a composite number }\right\} \text{ and } C= \left\{ x\in U|x-5\in U\right\}.\) Then find each of the following.
🔗
\(A\cap B, \, \left ( A\cup B \right )\cap C, \, \left ( A-B \right )-C,A-\left ( B-C \right ), \,A-\left ( B-C \right ), \, \left ( A-C \right )-\left ( B-A \right ), \, A'\cap B'\cap C'\)
🔗
🔗
8.
Let \(A\cup B=\left\{ a,b,c,d,e,x,y,z\right\} \text{ and } A\cap B=\left\{ b,e,y\right\}.\)
  1. If \(B-A=\left\{ x,y\right\} \text{ then } A = \)_______________
    🔗
    🔗
  2. If \(A-B=\phi, \text{ then } B = \) _______________
    🔗
    🔗
  3. If \(B=\left\{ b,e,y,z\right\}, \text{ then } A-B = \)_________________
    🔗
    🔗
🔗
🔗
9.
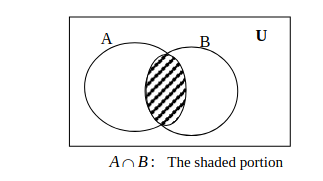
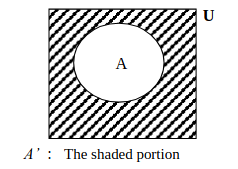
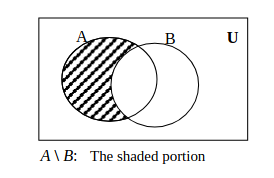
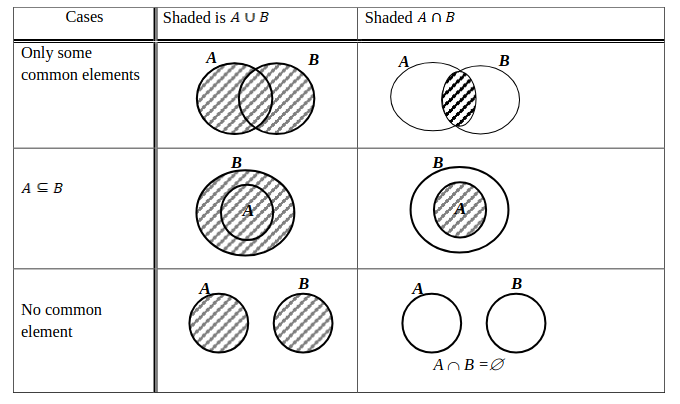
Let \(U=\left\{ 1,2,...,10\right\},\,A=\left\{ 3,5,6,8,10\right\},\, B=\left\{ 1,2,4,5,8,9\right\},\, C=\left\{ 1,2,3,4,5,6,8\right\} \text{ and } D=\left\{ 2,3,5,7,8,9\right\}.\) Verify each of the following.
  1. \(\displaystyle \left ( A\cup B \right )\cup C=A\cup \left ( B\cup C \right ).\)
    🔗
    🔗
  2. \(\displaystyle A\cap \left ( B\cup C\cup D \right )=\left ( A\cap B \right )\cup \left ( A\cap C \right )\cup \left ( A\cap D \right ).\)
    🔗
    🔗
  3. \(\displaystyle \left ( A\cap B\cap C\cap D \right )'= A '\cup B' \cup C' \cup D' .\)
    🔗
    🔗
  4. \(\displaystyle C-D=C\cap D'.\)
    🔗
    🔗
  5. \(\displaystyle A\cap \left ( B\cap C \right )'=\left ( A-B \right )\cup \left ( A-C \right ).\)
    🔗
    🔗
🔗
🔗
10.
Depending on question No.9 find.
  1. \(\displaystyle A \Delta B.\)
    🔗
    🔗
  2. \(\displaystyle C \Delta D.\)
    🔗
    🔗
  3. \(\displaystyle \left ( A \Delta B \right )\Delta D\)
    🔗
    🔗
  4. \(\displaystyle \left ( A \cup B \right )\setminus \left ( A \Delta B \right )\)
    🔗
    🔗
🔗
🔗
11.
For any two subsets \(A \text{ and } B\) of a universal set \(U,\) prove that:
  1. \(\displaystyle A \Delta B = B \Delta A .\)
    🔗
    🔗
  2. \(\displaystyle A \Delta B = \left ( A\cup B \right )-\left ( A\cap B \right ).\)
    🔗
    🔗
  3. \(\displaystyle A \Delta \phi = A.\)
    🔗
    🔗
  4. \(\displaystyle A \Delta A = \phi .\)
    🔗
    🔗
🔗
🔗
12.
Draw an appropriate Venn diagram to depict each of the following sets.
  1. \(U = \) The set of high scool students in Addis Ababa.
    🔗
    \(A = \) The set of female high school students in Addis Ababa.
    🔗
    \(B = \) The set of high school anti-AIDS club members students in Addis Ababa.
    🔗
    \(C = \) The set of school Nature Club members students in Addis Ababa.
    🔗
    🔗
  2. \(U = \) The set of integers
    🔗
    \(A = \) The set of even integers.
    🔗
    \(B = \) The set of odd integers.
    🔗
    \(C = \) The set of multiples of 3.
    🔗
    \(D = \) The set of prime numbers.
    🔗
    🔗
🔗
🔗
🔗

Checkpoint 1.4.43.

Add review
 7 
docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FPropositional-Logic-and-Set-Theory-%28NS-and-SS%29%2FSet-operations-and-Venn-diagrams%2FFind-the-number-of-students-who-played-one-sport-using-the-venn-diagrams.xml&entry.2077830997=source%2Fpropositional-logic-and-set-theory%2Fsections%2Fsubsections%2Fsec-set-theory%2Fsubsec-set-operations-and-venn-diagrams.ptx
🔗

Checkpoint 1.4.44.

Add review
 8 
docs.google.com/forms/d/e/1FAIpQLSfSNI6CXkmgeSZJh6v0WKkeD9MJ9g4pEQ9r0JaowD4ovNxj5w/viewform?usp=pp_url&entry.699375810=questions%2Ftop%2FMathematics-for-NS-%26-SS-23-24-Question-Bank%2FPropositional-Logic-and-Set-Theory-%28NS-and-SS%29%2FSet-operations-and-Venn-diagrams%2FIdentify-set-operation-in-shaded-venn-diagram.xml&entry.2077830997=source%2Fpropositional-logic-and-set-theory%2Fsections%2Fsubsections%2Fsec-set-theory%2Fsubsec-set-operations-and-venn-diagrams.ptx
🔗
🔗
🔗
PrevTopNext